Информатика. 2 класс Демо+методичка

Уроки 28–29. «Таблица для мешка (по двум признакам)»

Мешки-векторы

Ребята уже знакомы с мешками и одномерными таблицами для мешков. Надеемся, что работа с данными математическими объектами не вызовет у учащихся особых трудностей. Однако для математики введение этих объектов оказалось достаточно важным шагом. Дело в том, что числа, прежде всего натуральные, очень удобны для измерений, например, времени (скажем, в секундах), или веса (в граммах), или пройденного расстояния (в метрах). Но если мы хотим указать, не сколько мы прошли, а куда пришли, то ситуация становится сложнее. Нам приходится указывать два «измерения» – два числа или два символа. Это похоже на то, как мы указываем положение в городе (например, говорим: «угол Ленина и Розы Люксембург») или поле на шахматной доске (например, e2). Самый распространённый в математике способ состоит в том, что на поверхность наносится сетка, как на бумаге в клетку. Если взять лист клетчатой бумаги, то с каждой клеткой на нём можно сопоставить два натуральных числа. Одно из этих чисел означает, сколько шагов надо сделать из нашей клетки, чтобы оказаться у левого края листа, а другое – сколько шагов надо сделать, чтобы добраться до нижнего края. Два таких числа называют координатами квадратика, их нельзя поменять местами – это не просто мешок, в котором лежат два числа, но упорядоченная пара (цепочка!), о которой мы договорились, что первое число – всегда расстояние до левого края листа, а второе – расстояние до нижнего края.

Тем не менее, координаты можно сложить в мешок. Для этого понадобятся бусины двух типов: бусина одного типа будет обозначать один шаг влево, а бусина другого – один шаг вниз. Какими именно будут бусины – вопрос договорённости. Например, квадратными и круглыми или синими и зелеными. А могут быть карточки, на которых написано «влево» и «вниз». Таким образом, каждой клетке на листе можно сопоставить мешок, в котором будет сколько-то бусин «влево» и сколько-то бусин «вниз».

Построив одномерную таблицу такого мешка, получим пару чисел, аналогичную координатам: ведь в таблице для каждого числа ясно, число каких именно карточек оно обозначает. Получится так называемый вектор. Конечно, вектор может иметь не только два, но и больше параметров (соответствующая цепочка чисел может быть длиннее). И в нашем мешке могут тоже лежать бусины многих типов. В отличие от множества в мешке (мультимножестве) может быть несколько объектов одного типа. Значит, в таблице для мешка будут не только единицы и нули.

С понятия вектор начинается изучение науки, которую называют аналитической геометрией. Данное понятие лежит в фундаменте всей физики и многих разделов математики.

Тема данного урока – двумерные таблицы для мешков. С научной точки зрения двумерные таблицы – это следующая по сложности структура, набор векторов. Конечно, мы не будем наших детей сейчас нагружать этой сложной терминологией. Достаточно того, что они научатся сортировать и классифицировать элементы мешка по двум признакам и аккуратно заполнять таблицу.

Лист определений «Таблица для мешка (по двум признакам)»

На этом уроке ребята знакомятся с таблицей для мешка нового вида. До настоящего момента детям встречались лишь такие таблицы, в которых все элементы мешка делятся по одному признаку. Такие таблицы можно называть одномерными. Например, бусины в мешке можно делить по форме и составлять соответствующую таблицу. Можно составить другую одномерную таблицу, разделив все бусины по цветам. Наконец, можно составить третью одномерную таблицу для мешка бусин, посчитав число одинаковых бусин каждого вида (определенной формы и цвета).  Даже если бы мы в одной задаче составили все три таблицы, то задача изменилась бы только количественно, ведь составляя каждую таблицу мы все равно принимаем во внимание только один признак, то есть все признаки мы рассматривали до настоящего урока по отдельности.

На этом уроке ситуация меняется качественно. Так составляя таблицу на листе определений, мы одновременно принимаем во внимание два признака бусин – их форму и цвет. В результате в последней таблице листа определений каждое число указывает нам, сколько в мешке лежит бусин данной формы и данного цвета. В этом примере формы мы пишем по горизонтали (в названиях столбцов), а цвета – по вертикали (в названиях строк). Это совершенно не принципиально, можно делать и наоборот.

Решение задач из учебника

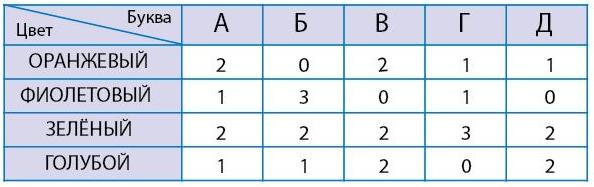
Задача 186. Заполняя таблицу для мешка П, можно воспользоваться тем же способом, который был подробно описан на листе определений. Так, можно разделить все буквы по написанию, а уже затем делить все буквы одной формы по цветам (можно сделать и наоборот). Например, обведем в мешке все буквы А (лучше делать это карандашом). Теперь среди обведенных букв ищем и считаем буквы каждого цвета. Посчитанные буквы сразу помечаем галочкой, а соответствующие числа сразу заносим в первый столбец таблицы. Получаем, что среди букв А: две оранжевых, одна фиолетовая, две зеленых и одна голубая. Теперь можно также поработать с буквами Б, затем – с буквами В и т. д. В результате получаем таблицу для мешка П по двум признакам – цвету и написанию (форме) букв.

Ответ:

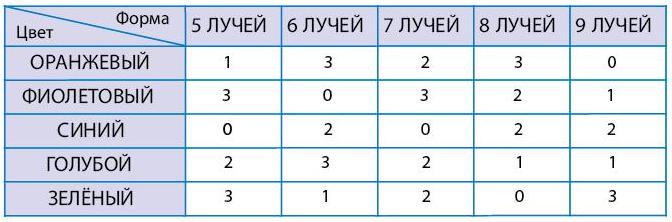
Задача 187. Как видите, все фигурки в мешке Т – правильные звезды (все стороны этих звезд равны). Поэтому по форме звезды отличаются только за счет различия в количестве лучей. Кроме того, звезды различаются цветом. Решать эту задачу дети могут так же, как и предыдущую, но она несколько сложнее технически. Дело в том, что детям, скорее всего, окажется сложно различить звезды по форме на глаз – придется считать в каждой из них число лучей. Одновременно считать число лучей и число самих звезд под силу далеко не всем детям (да и взрослым, тоже), кто-то из детей будет постоянно сбиваться. Поэтому можно дать детям такой совет – сначала посчитать во всех звездах в мешке число лучей и подписать его рядом с каждой звездой. Дальше делим звезды по цветам и для каждого цвета считаем число звезд каждой формы, заполняя соответствующий столбец таблицы. 

Ответ:

Задача 188. Несложная задача на повторение значений истинности утверждений. Среди этих утверждений ровно 2 истинных и 2 ложных.

Задача 189. В мешках К, Л и М есть одинаковые цифры, поэтому кто-то из ребят может запутаться при построении их суммы. В этом случае нужно посоветовать учащемуся соединить все цифры из мешка Н с такими же цифрами в мешках К, Л и М.

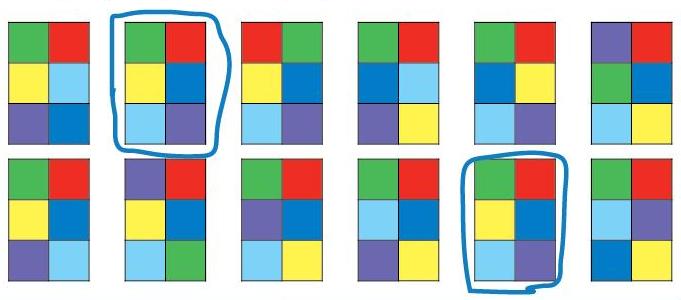
Задача 190. Необязательная. Как и во многих аналогичных задачах здесь удобно использовать классификацию по цветам соответствующих клеток и делить фигурки на группы. Например, возьмем крайние правые верхние клетки всех фигурок и сравним их. Видим, что всех фигурках кроме одной эти клетки красные, значит, фигурку с зеленой клеткой можно убрать из рассмотрения (и вычеркнуть). Теперь рассмотрим крайние левые верхние клетки всех оставшихся фигурок.  В двух фигурках эти клетки фиолетовые, в остальных – зеленые. Две фигурки с крайней левой фиолетовой клеткой – разные (их тоже можно вычеркнуть), значит будем искать одинаковые среди  оставшихся фигурок. Так будем разбивать на группы и вычеркивать неподходящие фигурки и дальше, пока в одной из групп не останется ровно 2 одинаковые фигурки.

Задача 191. В этой задаче детям предстоит закончить раскрашивание бусин в мешке так, чтобы мешок соответствовал таблице. При этом желательно соблюдать следующие правила. Первое – лучше всего использовать клетки таблицы по очереди, в определенном порядке. Например, по строкам слева направо и сверху вниз. Второе – лучше помечать клетку таблицы, которую мы уже использовали. Так, берем первую клетку первой строки таблицы – в мешке должно быть 3 синие квадратные бусины. У нас в мешке уже есть одна такая бусина, значит нужно раскрасить синим еще две квадратные бусины. После этого первую клетку первой строки таблицы помечаем галочкой (мы ее уже использовали) и переходим ко второй клетке первой строки таблицы и т. д., пока клетки в таблице у нас не закончатся. После этого все бусины в мешке должны оказаться раскрашенными.

Задача 192. Обратите внимание, что в этой задаче мешков несколько меньше, чем цепочек. Проследите, чтобы для каждого слова нашелся мешок.

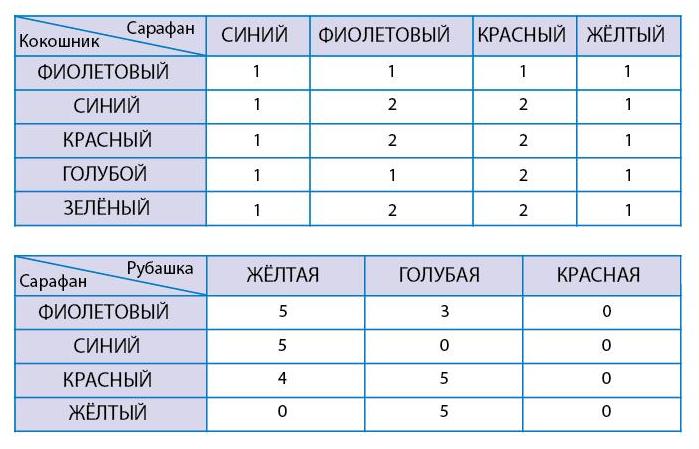
Задача 193. Отличие данной задачи от задач 186 и 187 в том, что здесь нужно заполнить не одну, а две таблицы для мешка фигурок. Как видите, фигурки здесь отличаются по 3 признакам: цвет сарафана, цвет кокошника, цвет рубашки. Взяв каждые два признака, можно составить двумерную таблицу для этого мешка. Интересно, что во второй таблице в последнем столбце будут стоять одни нули, поскольку фигурок в красных рубашках у нас просто нет. Кто-то из детей заметит это сразу и заполнит последний столбец, но большинство, скорее всего, заметит это только в процессе поиска и подсчета соответствующих фигурок. Нам думается, что решение этой задачи никак комментировать не нужно, а вот проверку лучше обсудить (хотя бы в индивидуальном порядке). В частности, хорошо бы обратить внимание детей на связь двумерных таблиц между собой. В данном случае для правильного решения задачи должны выполняться следующие условия. Первое – общее число фигурок в обеих таблицах должно быть одинаковым. Второе –  сумма чисел в столбцах первой таблицы равна сумме чисел во второй таблице. Хорошо бы попросить всех детей, которые возьмутся за эту задачу, сначала проверить соблюдение этих двух условий, а уже затем устраивать фронтальную проверку.

Ответ:

Задача 194. Дети, конечно же, уже не раз строили мешок по его одномерной таблице. Здесь, однако, задача усложняется: в процессе построения мешков надо постоянно следить за соблюдением дополнительных условий. К тому же эти условия функционируют с отрицанием (как ложные). При построении первого мешка необходимо следить лишь за тем, чтобы в мешке не оказалось одинаковых бусин. Поэтому все три синие бусины должны быть разных форм и все три зеленые – тоже. Две красные бусины должны быть тоже разных форм. При построении второго мешка приходится учитывать не только это условие, но еще и то, чтобы мешок не был таким же, как уже построенный. Как видим, это можно сделать только за счет красных бусин. Поэтому во второй мешок надо обязательно положить красную бусину, которой нет в первом мешке.

Задача 195. Здесь проблема в том, что в наборе слишком много одинаковых цифр. Кроме того, ребятам по ходу решения необходимо отделять цифры от букв.

Задача 196. Необязательная. Эта задача обратная к задаче 184. Здесь необходимо по данным утверждениям выяснить, кто из ребят в какой день родился. Проще всего выяснить даты рождения Маши и Коли, ведь среди наших дат только две отличаются ровно на 2 дня. Значит Маша родилась 21 марта, а Коля – 23 марта. Петя родился в мае, а Таня младше Пети, значит Петя родился 4 мая, а Таня – 19 мая. Теперь становится понятно, когда родилась Нина (при этом предпоследнее утверждение оказывается истинным автоматически).

Задача 197. Необязательная. В этой задаче мы хотим обратить внимание ребят на то, что в русском и латинском алфавите имеются совпадающие символы. Вопрос этот (как мы уже говорили) довольно тонкий, поэтому мы даем ребятам подсказки в виде указания соответствующих букв латинского алфавита. Поскольку соответствующие русские и латинские буквы выглядят совершенно одинаково, то приходится различать их указанием на место в соответствующем алфавите. Так первая буква латинского алфавита такая же, как первая буква русского алфавита (А), а пятнадцатая буква латинского алфавита такая же, как шестнадцатая буква русского алфавита (О).  Конечно, в этой задаче не содержится полный список совпадающих букв. Если детей это заинтересовало, можете продолжить эту работу и составить полный список. Напомним, что в этой задаче (как и в большинстве задач нашего курса) мы рассматриваем буквы исключительно как символы, поэтому считаем одинаковыми буквы, которые выглядят одинаково. В языке, каждая буква помимо своего начертания несет с собой целый ряд языковых свойств, в частности, обозначает в словах некоторые звуки, имеет свое название и т. д. В этом смысле русская буква Н и латинская Н – совершенно разные. Но мы оставляем практически весь языковой контекст за пределами нашего курс, почти также мы поступаем и со словами. Конечно, обсуждать все это с детьми не нужно, но нужно иметь это в виду при установлении межпредметных связей. Здесь наш и языковой подход к буквам сильно различаются, и проводить какие-либо параллели нужно очень осторожно.

Задача 198. Необязательная. Большинству детей в случае затруднения можно здесь посоветовать  сначала собрать на столе мешок бусин цепочки (мешок N), а затем делать пробы, переставляя бусины до тех пор, пока все утверждения не станут истинными.

Задача 199. Необязательная. Задача на повторение темы «Одинаковые фигурки». В случае затруднения здесь можно предложить ребенку использовать перебор или деление букв на группы. Слабому учащемуся можно выдать греческий алфавит и предложить двигаться по строкам фигурок, вычеркивая одновременно буквы из набора и из греческого алфавита. В какой-то момент в наборе встретится буква, которая из алфавита уже вычеркнута, значит, такая же буква в наборе уже встречалась.

Вот греческие буквы с их названиями:

Компьютерный урок « Таблица для мешка», 1 часть

Решение задач 196 – 203

Задача 196. При решении задачи на заполнение таблицы для мешка, чтобы не запутаться, лучше сразу выбрать некоторую стратегию учета фигурок. Одна из стратегий описана на листе определений. Вторая стратегия состоит в следующем. Берем любую фигурку из мешка, например, красный лимон. Обводим в мешке все красные лимоны красным, считаем, сколько фигурок обведено красным и заполняем клетку таблицы «красные лимоны». Теперь выбираем любую не обведенную фигурку в мешке, например, зеленое яблоко. Обводим все зеленые яблоки новым цветом и считаем, сколько фигурок мы обвели, заполняем клетку «зеленые яблоки». Так продолжаем до тех пор, пока все фигурки в мешке не окажутся помеченными (если цвета линий обводки в мешке начнут повторяться, можно начать помечать фигурки галочками).

Задачи 197. При построении мешка по таблице лучше всего использовать клетки таблицы по очереди, в определенном порядке. Например, по строкам слева направо и сверху вниз. Кроме того, можно помечать клетку таблицы, которую мы уже использовали. Так берем первую цифру в первой строке: кладем в мешок одну красную треугольную бусину и помечаем первую клетку таблицы галочкой. Дальше переходим ко второй цифре в первой строке и т.д., пока не дойдем до последней цифры в последней строке.

Задача 198. Решений здесь конечно много. При построении цепочки очень важно помнить, что для истинности утверждения необходимо, чтобы оно имело смысл, то есть каждая фигурка, о которой идет речь, должна встречаться в цепочке ровно 1 раз.

Задача 199. Эту задачу можно решать методом проб и ошибок – компьютерная «лапка» позволяет реализовывать многочисленные пробы достаточно легко. Однако, пробы можно существенно сократить, если внимательно прочитать условие задачи и сделать некоторые выводы. Например, в условии сказано, что шестая бусина после красной должна быть желтой. В нашей цепочке всего 7 бусин, значит соблюсти данное условие можно только в том случае, если поставить красную бусину первой в цепочке, а желтую бусину (пока любую) – последней. Теперь проанализируем другую часть условия, и поставим зеленую бусину предпоследней и любую треугольную бусину – второй в цепочке. Остальные бусины могут при этом стоять не любых местах.

Задача 200. В целом эта задача аналогична компьютерной задаче 197, но таблица здесь несколько больше. Если учащийся при построении мешка будет затрудняться или допускать ошибки, посоветуйте ему помечать использованные клетки таблицы (подробней см. комментарий к задаче 197).

Задача 201. Задача на повторение сравнения фигурок наложением.

Задача 202. Эта задача является частично лингвистической, поскольку кроме договоренностей, введенных в нашем курсе, здесь работают языковые (неформальные) соображения. Например, в задаче речь идет только о словах русского языка. В отличие от понятия «слово», введенного в нашем курсе (как любой цепочки букв) понятие «слово русского языка» крайне сложно объяснить формально и еще сложнее определить в спорных случаях, является цепочка словом русского языка или нет. Лингвистическая направленность задачи порождает некоторые трудности с поиском формального алгоритма решения. Действительно, можно предложить детям сначала составить все возможные цепочки из данных букв, например, из букв слова АНИС, а затем из всех этих цепочек выбрать ту, которая является словом русского языка. Но это довольно долгий путь. Он может осложняться дополнительно тем, что ребенок по каким-то причинам вообще не знает слова САНИ (то есть оно для ребенка словом русского языка не является). Все эти рассуждения мы приводим не для того, чтобы убедить вас, что эта задача очень сложная. Наоборот, вы убедитесь, что некоторые дети решили ее очень быстро, буквально на несколько секунд. Тем не менее, наверняка найдутся дети, которые застрянут на некоторых (или даже на всех) словах. Не надо относиться к этому слишком серьезно, учитывая приведенные выше соображения. То, что ребенок не решает данную задачу не значит, что он не знает материал курса. Относитесь к этой задаче на треть как к развлекательной (на сообразительность), на треть – как к языковой и лишь на треть – как к информационной.

Задача 203. Необязательная. Как всегда в задачах, которые содержат ложные утверждения, дети либо действуют методом проб и ошибок, либо строят отрицания утверждений. Во втором случае у них получается следующий набор утверждений, которые должны быть истинными: «В цепочке кошка идет не позже белки», «В цепочке следующая фигурка после рыбы – не бабочка», «В цепочке пятая фигурка с конца – не заяц». При любом способе решения дети обязательно должны учесть все условия, при которых данные утверждения имеют смысл, а именно: в цепочке должна быть ровно одна кошка, ровно она белка, ровно одна рыба, кроме того рыба должны стоять в цепочке не последней и в цепочке должно быть не меньше 5 фигурок.

Компьютерный урок « Таблица для мешка», 2 часть

Решение задач 204 – 210

Задача 204. В этой задаче ребята повторяют одномерную таблицу для мешка. Некоторая сложность при решении этой задачи состоит в том, что в шапке таблицы буквы указаны не графически, а своими названиями. Это сделано специально, чтобы ребята здесь были вынуждены вспомнить русские названия латинских букв. Некоторые дети, наверняка, будут при этом путать названия русских и латинских букв (например, считая что «эс» – название буквы «С»). Таких придется для начала попросить установить соответствие между буквами мешка и их названиями в таблице, а после этого снова вернуться к решению задачи.

Задача 205.На первый взгляд задача кажется необычной, но по содержанию является не сложной. Действительно, первое задание состоит в том, чтобы расставить в клетках таблицы числа. Это можно делать совершенно произвольно, главное, чтобы их сумма была не меньше 10, но не больше 20. Второе задание – построить по таблице мешок, является для детей привычным.

Задача 206. В силу первого утверждения бусин в цепочке может быть как семь, так и три. Но в настоящий момент дети должны понимать, что второе утверждение может быть истинным только в том случае, если бусин в цепочке будет не меньше шести. В противном случае пятой бусины даже после первой бусины цепочки не будет, и для любой бусины в цепочке утверждение не будет иметь смысла. Отсюда следует вывод – в этой цепочке бусин либо шесть, либо семь. В первом случае оранжевая круглая бусина может быть только первой, во втором – первой или второй. Заметим, что из истинности второго утверждения также следует, что оранжевая круглая бусина в этой цепочке ровно одна. Теперь проанализируем третье утверждение. В ходе проб и ошибок (либо рассуждений) приходим к выводу, что оранжевая бусина, о которой идет речь в третьем утверждении не может быть той же самой, которая у нас уже есть в цепочке. Значит это другая бусина, которая не может быть круглой – она квадратная или треугольная. Теперь остается вставить в нашу цепочку кусок: оранжевая (квадратная или треугольная) - … - фиолетовая треугольная. На оставшихся местах цепочки можно поставить любые бусины, кроме оранжевой круглой и фиолетовой треугольной.

Задача 207. Здесь можно поставить на второе и четвертое место буквы О, поскольку в мешке Д имеются только две одинаковые буквы. Что касается третьего утверждения, то вариант здесь тоже всего один – поставить буквы С первой, а Й – последней. Теперь попробуем правильно поставить в цепочку букву Е. Кроме Е гласных в нашем мешке всего две – это буквы О. Второе место после первой по счету О уже занято, значит мы можем поставить букву Е только на второе место после второй буквы О. После этого места для букв Л и В тоже определяются однозначно. Получаем единственное решение – слово СОЛОВЕЙ.

Задач 208. Аналогичную задачу (для русских букв) ребятам уже приходилось решать (см. комментарий к компьютерной задаче 79). 

Задача 209. Это первая задача на поиск слова в Словаре, в который встречается условие «Буквы в этом слове стоят в алфавитном порядке». Это условие может показаться детям необычным. В алфавитном порядке мы можем расставить только разные буквы (непонятно, как упорядочить в алфавитном порядке две одинаковые буквы), поэтому первое условие является как бы необходимым для того, чтобы предлагать детям третье. На самом деле в русском языке сравнительно мало слов, в которых буквы идут в алфавитном порядке. В этом дети убедятся, просматривая слова из Словаря. В значительной степени это связано с закономерностями встречаемости гласных в русских словах. Например, не подходят все слова, в которых есть буква А и она стоит не первой (а таких в русском языке очень много). Во многих словах есть две одинаковые гласные, а слова, в которых имеются одинаковые буквы, нам не подходят изначально. Рассмотрим слова из Словаря на букву А. Слова: АВАРИЯ, АНГИНА, АПТЕКА, мы отбрасываем сразу (в них есть одинаковые буквы). Слово АВГУСТ не подходит, так как буквы С и Т в нем стоят позже У (в алфавите, наоборот). Слово АДРЕС не подходит, так как в нем буква Е стоит позже Р (в алфавите, наоборот). В результате, просмотрев все слова на буквы А – Д мы не находим в Словаре ни одного подходящего слова. Первое по счету подходящее слово – ЕЛЬ. Дальше находим подходящие слова: ЕСТЬ, ЁЖ, ЁРШ.

Задача 210. Необязательная. У кого-то из ребят получится собрать эти кошельки методом проб и ошибок, но тем, кто запутался или затрудняется с решением, вам придется помочь организовать перебор монет. Перебор лучше начинать с самых крупных монет. Сколько может быть в кошельке монет по 10 рублей? Ясно, что одна или не одной. Положим в кошелек одну 10-рублевую монету и попробуем достроить его по условию методом проб и ошибок. В ходе этих проб мы понимаем, что не нужно использовать монеты в 5 рублей, и собираем оставшиеся 8 рублей 5 монетами в 1 рубль и в 2 рубля. Получаем первый мешок: 10 рублей, 2, рубля, 2 рубля, 2 рубля, 1 рубль, 1 рубль. Теперь не будем использовать монеты в 10 рублей. Сколько в кошельке может быть монет в 5 рублей. Ясно, что три, две, одна или не одной. Для каждого случая пытаемся построить решение, и для первых двух случаев это получается.

Решение задачи урока 6  для «Водолея»

Задача 1 (Водолей). Один из вариантов решения состоит в том, чтобы получить 8 литров, вылив в 21-литровый сосуд 4 литра, а потом еще 4 литра. Получить 4 литра можно, если 4 раза налить в 16-литровый сосуд из 5-литрового. После этого в 5-литровом сосуде останется ровно 4 литра.