Информатика. 2 класс Демо+методичка

Уроки 25–26. «Разбиение мешка на части»

На данном уроке ребята знакомятся с еще одной операцией над мешками – разбиением мешка на части. Из материала листа определений нетрудно понять, что разбиение мешка – операция, обратная сложению мешков, отсюда вытекают и ее основные свойства. Примеры листа определений позволяют детям сделать еще один важный вывод – в отличие от результата сложения мешков, который исходные мешки определяют однозначно, для одного мешка можно построить несколько разбиений. Так, для мешка Ю на листе определений построено два разбиения, одно из которых содержит пустой мешок, но, конечно, таких разбиений существует гораздо больше. Чтобы как-то сузить область решения при построении разбиения, мы чаще всего будем просить ребят построить разбиение, удовлетворяющее каким-то условиям, то есть разбиение по описанию.

Данный лист определений, несмотря на свою простоту, играет в курсе очень важную роль. Нетрудно догадаться, что операция разбиения мешка напрямую связана с темой «Классификация», в частности с классификацией элементов мешка. Собственно, разбиение мешка по некоторому принципу как раз и является классификацией.

Решение задач из учебника

Задача 160. В этой задаче ребята строят произвольное разбиение мешка, произвольность разбиения подчеркивается в условии словами «какое хочешь разбиение». Важно убедиться, что все ребята поняли содержание новой операции, именно для этого в задаче приведено указание к проверке. В ходе выполнения проверки ребята еще раз должны проверить, что:

а) в мешках В и Г лежат все бусины из мешка Б;
б) в мешках В и Г нет никаких других бусин.

Самый простой способ в этом убедиться – соединить все бусины из мешка Б в пары с бусинами из мешков В и Г. Если у кого-то из учеников возникли существенные трудности с выполнением разбиения, лучше всего перейти на телесный уровень, то есть собрать из бусин на столе мешок Б, разделить его бусины на две любые части, наклеить получившиеся части в мешки В и Г.

В этой задаче мы также обращаем внимание детей на связь между операцией разбиения мешка и действием вычитания, которое происходит над количеством элементов мешков по ходу разбиения. Чтобы операция разбиения была выполнена правильно, равенства, приведенные в задаче, обязаны быть верными.

Задача 161. В данной задаче учащемуся необходимо проделать операцию, обратную ссыпанию – восстановить цепочку (слово) по мешку ее букв. Однако, как уже известно детям, по мешку бусин цепочка не восстанавливается однозначно, нужно указание дополнительных условий. В данной задаче два дополнительных условия: последняя буква цепочки – Ч и должно получиться слово из Словаря. Поиск слова в Словаре может оказаться нелегким, поскольку там слова упорядочены по первой букве, а нам известна – последняя. Видимо проще всего – выполнить перебор по всем оставшимся буквам в мешке (кроме Ч), поочередно ставя их на первое место и пытаясь найти слово в Словаре из 7 букв с последней Ч. Такое слово в Словаре оказывается одно, проверяем его по мешку букв и убеждаемся, что найденное слово ЦАРЕВИЧ – решение.

Задача 162. Необязательная. В процессе решения этой задачи и других подобных задач можно выделить следующие этапы:

а) анализ всех утверждений;
б) планирование (установление порядка рассмотрения утверждений);
в) рассмотрение каждого утверждения в соответствии с планом и постепенное сужение круга подходящих слов до единственного.

Здесь удобно сначала использовать последнее утверждение и найти в Словаре все слова на букву Р. Затем можно использовать второе утверждение задачи и выбрать все слова (из слов на Р) с последней буквой А. Таких оказывается всего три. Наконец, первое утверждение будет истинно только для одного из них (слова РОМАШКА).

Задача 163. Если у кого-то из ребят возникнут проблемы с построением мешка, посоветуйте ему решать задачу в телесно-графическом режиме, методом проб и ошибок. Для этого нужно собрать из бумажных бусин мешок К, а затем выделить из его бусин 6 разных бусин. Они и будут составлять мешок Л.

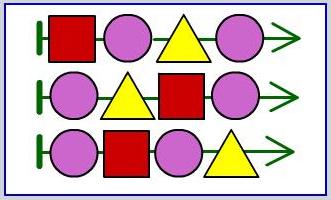
Задача 164. Здесь ребятам нужно построить две разные цепочки по одному описанию. Из данных утверждений можно сделать вывод, что в каждой подходящей цепочке должны быть 2 фрагмента: красная квадратная – фиолетовая круглая и фиолетовая круглая – желтая треугольная. Эти фрагменты могут стоять в разном порядке, отсюда и разные цепочки. Кроме того, можно составить два фрагмента в один, удовлетворяющий сразу двум условиям: красная квадратная – фиолетовая круглая – желтая треугольная. Всего цепочек, соответствующих данному описанию можно построить ровно 3:

Задача 165. Необязательная. Здесь первая буква слова не известна, но между словами ХВОРОСТ и ЧАЙНИК в Словаре оказывается не так уж много слов. Из них только в двух словах есть буквы Л и А – ХУЛИГАН и ЦАПЛЯ.

Задача 166. В этой задаче ребята выделяют часть мешка по описанию. Часто такие описания строятся сходным образом – указывается, какие объекты должны лежать в мешке и сколько таких объектов должно там лежать. В данном случае дети выделяют мешок всех гласных букв, которые лежат в мешке К.

Задача 167. Необязательная. Здесь, как и в задаче 165, сначала необходимо выбрать из Словаря цепочку слов, среди которых есть смысл вести более тщательный перебор (цепочка слов от слова КОНЕЦ до слова ЩЕНОК). Теперь среди выделенных слов нужно найти слово из пяти букв с третьей буквой Н. Так находим слово СИНЕЕ.

Задача 168. Эта задача несколько напоминает задачу поиска двух одинаковых мешков и решается с применением тех же приемов. Один из них – деление слов на группы и сравнение мешков букв уже по группам. Например, в данной задаче сначала можно разделить слова на группы по числу букв в слове. Так мы сразу отбросим слова ПОМИДОР и ПУДЕЛЬ. Оставшиеся слова (из 8 букв) можно делить на группы по наличию/отсутствию некоторых букв. В конце концов, в каждой группе останутся по 2–3 слова, которые несложно сравнить между собой. Так мы находим пару нужных слов – АПЕЛЬСИН и СПАНИЕЛЬ.

Задача 169. Поскольку раскрасить здесь предлагается только одну бусину, значит три одинаковые бусины среди раскрашенных бусин уже есть. Поэтому начать решение имеет смысл с того, чтобы найти среди раскрашенных три одинаковые бусины. После этого сразу становится понятно, бусину какой формы следует раскрасить и в какой цвет.

Задача 170. Необязательная. Чтобы сделать две или больше цепочек одинаковыми, проще всего двигаться сразу по всем цепочкам от первой буквы. Видим, что первая буква в одной из цепочек – буква «Ч». Значит и в других цепочках на первом месте должна стоять «Ч», вписываем «Ч» в первые окна двух оставшихся цепочек. Теперь переходим ко второй букве и т. д. Видим, что в результате у нас получилось три одинаковых слова – слова «ЧЕМОДАН».

Задача 171. Здесь в условии сказано, что в искомой части мешка все бусины должны быть одной формы, но непонятно, какой формы бусины должны быть. Чтобы это понять, нужно привлечь условие о том, что в мешке должно быть, по крайней мере, 6 бусин. Теперь понятно, что нужно собирать в мешок треугольные бусины, ведь круглых бусин в исходном мешке всего три, а квадратных – всего две.

Задача 172. Здесь найти недостающие буквы хаотичным просматриванием маловероятно, поэтому придется организовать полный перебор русских букв. Перебор будет здесь заключаться в сопоставлении каждой буквы мешка с буквами алфавитной линейки. При этом, конечно, необходимо делать пометки. Берем любую букву из мешка, например А. Обводим ее в мешке и ставим галочку около соответствующей клетки алфавитной линейки. Теперь берем следующую букву, например Ц и т.д. Как только все буквы в мешке будут обведены, на алфавитной линейке окажутся непомеченными ровно 3 клетки. В этих клетках и будут недостающие буквы.

Задача 173. Если учащийся испытывает в этой задаче серьезные трудности, предложите ему написать все числа из мешка Ф на карточках или кусочках бумаги и раскладывать их по двум мешкам явно. Можно использовать при работе числовую линейку от 1 до 100.

Задача 174. Необязательная. Задача на повторение алгоритма подсчета областей картинки. Как видите, областей в этой картинке достаточно много. Однако они неплохо выделяются на глаз, поэтому данную задачу можно предлагать практически любому ребенку в классе, за исключением самых невнимательных и рассеянных.

Ответ: в этой картинке 15 областей.

Задача 175. Необязательная. Здесь вполне возможно найти одинаковые мешки без всякой системы, то есть случайным образом. Но даже если это не получилось, мешки здесь наглядно делятся на группы по наличию или отсутствию некоторой птицы. Так, в 4 мешках есть зеленая птичка, а в двух первых – ее нет. При этом первые два мешка разные, значит, их можно просто вычеркнуть. Среди оставшихся мешков в трех есть синяя птица, а в одном ее нет, значит, мешок E тоже можно вычеркнуть. Оставшиеся три мешка совсем несложно сравнить между собой.

Задача 176. Необязательная. Утверждений здесь достаточно много, причем многие связаны между собой. Удержать в голове столько утверждений детям бывает затруднительно. Самый оптимальный путь состоит в том, чтобы правильно выбрать утверждение, с которого лучше начать строить цепочку. Наиболее однозначную информацию здесь дают четвертое и пятое утверждения, с них и стоит начать. Поскольку нам известно, что букв в слове должно быть семь (как в мешке), то пятая с конца буква будет третьей с начала. Рисуем цепочку, в которой третья буква Т, а пятая И. Дальше можно использовать первое и второе утверждение и поставить после Т букву Н, а после И – букву Ц. Теперь ясно, что буквы П и Я можно поставить только на первое и второе место, а на оставшееся место – оставшуюся в мешке букву А. Получаем слово ПЯТНИЦА.

Компьютерный урок «Разбиение мешка на части», 1 часть

Решение задач 173 – 180

Задача 173. В этой задаче ребята выполняют разбиение мешка непосредственно, то есть так, как это выглядит при разбиении телесного мешка предметов на две части. В ходе этой работы дети раскладывают все предметы из одного мешка по двум другим мешкам. В аналогичных практических задачах учащиеся могут перекладывать предметы руками, в компьютерных задачах на разбиение мешка работают «лапкой». В данном случае разбиение не является произвольным, а подчиняется условию: все гласные буквы должны оказаться в одной части мешка, все согласные – в другой (знаков в мешке Б нет). С кем-то из ребят в процессе решения задачи, возможно, придется вспомнить, какие буквы в русском языке считаются гласными, а какие – согласными.

Задача 174. Для кого-то эта задача может оказаться технически сложной. Проблема в том, что фигурок в мешке много и они очень похожи, кто-то из детей здесь возможно просто запутается. Самый простой способ решения данной задачи – искать тройки одинаковых фигурок и сразу раскрадывать фигурки каждой тройки по трем разным мешкам. Если с поиском очередной тройки возникают проблемы, нужно посоветовать учащемуся, использовать полный перебор. Например, возьмем любую фигурку из мешка (можно сразу положить ее в мешок Р) и найдем в мешке Л еще две такие же фигурки, просматривая все фигурки в мешке Л по строкам. Найдя две нужные фигурки положим их в мешки С и О. После этого фигурок в мешке Л становится меньше, а значит перебор делать проще.

Задача 175. Обратите внимание на тех ребят, которые все еще путают латинские буквы с похожими русскими буквами, например, путают: Я и R, У и Y, И и N и проч.  . С такими ребятами стоит обсудить вопрос о различении русских и латинских букв подробно, держа перед глазами оба алфавита. Можете использовать для этого разговора материал из урока «Латинский алфавит» (текст «О названиях и начертаниях букв»).

Задача 176. В этой задаче дети на материале новой темы «Разбиение мешка на части» повторяют названия дней недели. Один из вариантов решения – перебор всех слов из мешка С сверху вниз. Если просматриваемое слово – название дня недели, то перекладываем его в мешок Н, если – нет, переходим к следующему слову (просмотренные слова из мешка С можно помечать галочками).

Задача 177. Здесь дети будут использовать для решения разные стратегии. Кто-то будет сразу сопоставлять пары римских и арабских чисел, кто-то будет записывать арабские числа римскими цифрами и затем искать в наборе такие же записи, а кто-то наоборот – будет записывать римские числа арабскими цифрами и затем соединять числа в пары. При возникновении проблем лучше всего посоветовать ребенку, вернуться к проекту «Римские цифры».

Задача 178. В этой задаче дети должны осуществить перебор всех слов, которые стоят в Словаре между словом ПЯТЬ и словом СЕНТЯБРЬ и найти все такие слова, в которых нет одинаковых букв. Таких слов оказывается всего шесть: РАЗНЫЕ, РЕБЁНОК, РУЧЕЙ, САПОГИ, СЕГОДНЯ, СЕМЬ.

Задача 179. Эта задача довольно сложная, поскольку в ней ребятам приходится использовать одновременно несколько условий и стыковать их между собой. Последнюю букву (Ь) можно поставить в слово сразу. Из четвертого и пятого утверждения следует, что в слове имеются два кусочка: Д – Р и Е – Л. Поскольку в слове всего 5 букв, осталось выяснить, какой из этих кусочков стоит в слове первым, а какой – вторым. На этот вопрос дает ответ третье утверждение. В результате мы получаем слово ДРЕЛЬ.

Задача 180. Необязательная. Это задачи комбинаторного характера. Действительно, нужно перебрать все возможные комбинации из 4 бусин (определенной формы) двух цветов. В данном случае комбинаций существует всего 9, а мешков у нас восемь, поэтому перебрать придется почти все комбинации и методом проб и ошибок (которым часто пользуются дети в таких задачах) это сделать удастся далеко не всем детям. Хорошо бы провести некоторые рассуждения, например такие. Рассмотрим пока две круглые бусины из мешков. Сколькими способами их можно раскрасить двумя цветами? Как видим тремя: обе зеленым, обе желтым и раскрасить две бусины в разные цвета. Та же ситуация будет и с двумя квадратными бусинами – существует 3 способа их раскраски в зеленый и желтый цвет. Теперь каждый из трех способов раскраски круглых бусин можно комбинировать с каждым из трех способов раскраски квадратных бусин. Получаем всего 3×3=9 возможных способов. Конечно, ваши дети пока не смогут провести такие рассуждения, и будут действовать методом проб и ошибок. Зато эти рассуждения могут помочь вам при работе с учеником, который запутался.

Компьютерный урок «Разбиение мешка на части», 2 часть

Решение задач 181 – 187

Задача 181. Кто-то из детей здесь использует некоторые арифметические, логические или практические соображения. Действительно, в мешке У монет должно быть меньше, а денег – больше, такой ситуации можно добиться только за счет монет большего достоинства. В мешке А есть лишь одна такая монета, значит монету в 5 рублей можно сразу положить в мешок У. Теперь положим в мешок Н на 2 монеты больше – три монеты. Поскольку в мешке остались только одинаковые монеты, выбора у нас, в сущности, нет. В мешке А монеты еще остались, их нужно разложить по мешкам поровну (тогда разница в 2 монеты так и останется). Теперь в мешке У стало 2 монеты, в мешке Н – 4 монеты, в мешке Н действительно на 2 монеты больше. Посчитаем сумму денег в каждом кошельке и проверим второе условие. Здесь описан только один из вариантов рассуждений, на самом деле их гораздо больше. Но если учащийся не знает, с чего начать, стоит посоветовать ему, воспользоваться методом проб и ошибок.

Задача 182. В этой задаче ребята осваивают операцию разбиения мешка на части и одновременно выполняют классификацию элементов мешка по форме.

Задача 183. В этой задаче возможны разные стратегии. Например, можно для каждого слова строить мешок его букв и сравнивать его с мешком S. Можно сравнивать с мешком S буквы каждого слова из мешка Y по очереди или же делить слова мешка Y на группы по наличию и числу некоторых букв, по ходу отбрасывая неподходящие. Например, можно сразу отбросить все слова с буквой А (в мешке S ее нет) и все слова с двумя буквами О (в мешке S одна буква О). Все оставшиеся слова оказываются подходящими.

Задача 184. Сложность здесь в том, что таблица обычно у нас строится для мешка, а здесь необходимо собрать цепочку. Действительно, как видим из условия таблица Б задает (в данном случае однозначно) мешок бусин искомой цепочки. Поэтому один из вариантов решений (методом проб и ошибок) заключается в том, чтобы для начала собрать (на рабочем поле) все бусины указанные в таблице. Теперь задача стала знакомой – собрать из бусин мешка цепочку, удовлетворяющую двум условиям (второму и третьему утверждению). Из второго утверждения следует, что вторая и четвертая бусины – красные треугольные, ведь в нашем наборе всего две одинаковые бусины. Из последнего утверждения следует, что первая и третья бусины квадратные, значит пятая бусина цепочки – желтая круглая. Поскольку цвет первой квадратной бусины может быть зеленым или синим, то задача имеет ровно 2 решения.

Задача 185. Эта задача очень похожа на задачу на построение мешка по двум его одномерным таблицам, только сформулирована она совсем иначе (из-за этого дети вряд ли увидят аналогию). Действительно, первое и второе утверждения о видах (формах) фигурок в мешке. В мешке должно быть 6 груш и 4 банана. Поскольку всего в мешке должно быть 17 фигурок, значит остальные 7 фигурок в мешке – яблоки. Так мы получили первую одномерную таблицу для мешка (по формам).

Третье и четвертое утверждение говорит нам о том, что в мешке должно быть: 7 зеленых и 5 желтых фигурок. Значит, оставшиеся 5 фигурок должны быть красными. Так мы получаем вторую одномерную таблицу для мешка (по цветам).

Поскольку все фрукты в библиотеке у нас имеются всех трех цветов, то эти таблицы оказываются независимыми друг от друга. Начинать можно с любой клетки любой таблицы и решений получается довольно много. Например, можно взять 7 зеленых яблок, 5 желтых груш, 1 красную грушу и 4 красных банана.

Задача 186. Без сомненья дети на уроках математики не раз расставляли числа в порядке возрастания. Однако, здесь числа записаны в римской нумерации и выполнить задание оказывается не так-то просто. Сначала необходимо перевести эти числа в арабскую форму записи, а уж потом выполнять задание. Кто-то сможет сразу разделить числа на группы (по возрастанию), а потом уже устанавливать порядок внутри групп. Так многим ребятам уже ясно, что числа, которые содержат знак «L» больше тех, которые его не содержат, значит, все числа с этим знаком можно положить в отдельную группу. Из оставшихся чисел те, которые начинаются с буквы «Х» больше, чем те, которые начинаются с «V» или «I». В результате числа разбиваются на 3 группы по следующему принципу: числа от 1 до 9, числа от 10 до 39, числа от 40 до 89. В каждой группе чисел оказывается уже меньше и их легче упорядочивать. Группу самых больших чисел можно еще разделить на две группы – числа, в которых «L» стоит первой (числа большие 50), и все остальные.

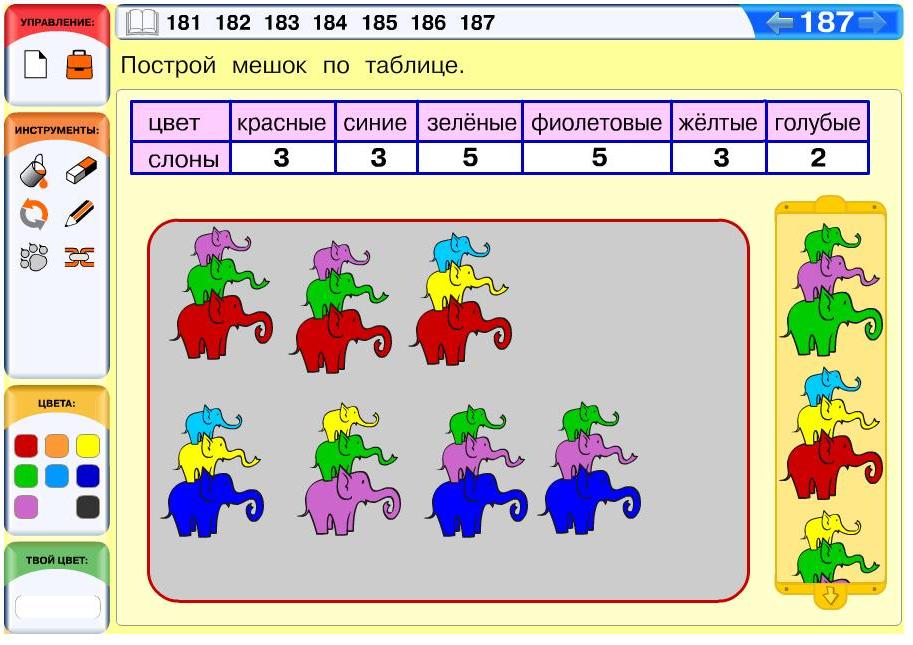
Задача 187. Необязательная. Хотя это задача на построение мешка по одномерной таблице, она достаточно сложная. Причина в том, что в мешке слоны лежат не по одному, а по три, причем в каждой тройке слоны разноцветные. За изменением числа слонов по цветам довольно сложно уследить. Как и другие аналогичные компьютерные задачи, эту задачу большинство детей будут решать методом проб и ошибок.

Решение задачи урока 5  для «Водолея»

Задача 1 (Водолей). Большинство детей по-прежнему продолжают решать подобные задачи методом проб и ошибок, выполняя различные команды с данными емкостями и глядя на то, что получилось. Так, если 4 раза налить в 11-литровую емкость из 3-литровой, то можно получить 1 литр. Значит, 7 литров здесь можно получить, налив в емкость (11-литровую или 14-литровую) 1 литр, затем 3 литра и еще 3 литра.