Информатика. 2 класс Демо+методичка

Уроки 23–24. «Латинский алфавит»

О названиях и начертаниях букв

В этом разделе мы обсудим несколько тонких вопросов, связанных с названиями и начертаниями русских и латинских букв. Как вы думаете, какого рода слово «икс»? А слово «дэ»? Вот что написано по этому поводу в русском переводе одной важной для всей математики ХХ в. книги: «Заметим, что в русском языке слова, служащие названиями букв латинского и греческого алфавитов и имеющие признак мужского или женского рода («икс», «дельта» и т. п.), фигурируют в двух формах: в форме склоняемого существительного соответствующего рода и в форме несклоняемого существительного среднего рода; в математической терминологии наблюдается тенденция к преимущественному употреблению второй формы» (Бурбаки Н. Теория множеств: Пер. с фр. - М.: Мир, 1965. - С. 53).

Названия букв русского языка, кроме таких, как «твердый знак» и «мягкий знак», – все среднего рода.

Вот вам еще один вопрос: какая буква здесь написана?  P

А здесь? Щ

В первом случае, чтобы правильно назвать букву, надо знать, что имеется в виду: не хватает дополнительной информации, чтобы понять, какая это буква – русская «эр» или латинская «пэ». Во втором случае это, скорее всего, русская «ща» (а может, это болгарская буква, которая читается «шт»?). Однако трудно понять, прописная это буква или строчная.

Как вы думаете, чем отличаются два символа    0  О и как каждый из них может называться в тексте на русском языке?

Конечно, буква О и нуль очень похожи друг на друга. На пишущих машинках это часто бывает один и тот же знак. Но есть машинки, в которых буква О и нуль разные. И буква О, и нуль - это эллипсы (или овалы), но обычно нуль более вытянут по сравнению с буквой О.

Обратите внимание на то, что некоторые буквы при очень большом внешнем сходстве все же различаются в начертаниях. Например, русская «ка» имеет вид К, а латинская «ка» – вид K (по-разному расположена правая нижняя «лапка»), русская «у» – вид У, а латинская «игрек» – вид Y. И потому написание БYДYТ (так иногда пишут на Западе в текстах для русскоязычных) выглядит так же противоестественно, как УOU (так иногда пишут в России для иностранцев). Вопрос этот стал еще более актуальным в связи с использованием компьютеров и компьютерных шрифтов, где, например, две абсолютно одинаковые на вид буквы С и C имеют два разных кода, так как одна из них – русская «эс», а другая – латинская «цэ».

Когда не было компьютеров, но в тексте надо было использовать римские цифры (строящиеся на основе латинского алфавита), то в русской машинописи часто использовали русскую У вместо латинской V и т. п. Получалось что-то вроде ХУШ для обозначения XVIII века. Замечательно, что и сейчас в компьютерном тексте на русском языке можно иногда встретить то же самое. Более того, поскольку теперь книги создают на компьютере, то этот прием «прокрался» и в книги! Вот какова сила привычки!

Если вам еще не надоели вопросы, то вот еще пара.

Какая буква латинского алфавита никогда не употреблялась в старых латинских текстах? Такой буквой является буква W («дубль-вэ»).

Буквы латинского алфавита тоже имеют названия в русском языке. Мысль о том, что латинские буквы имеют названия в русском языке (а не в латинском, французском, немецком и других языках с латинской графикой), подчас оказывается неожиданной даже для специалистов. Русские названия для греческих букв почему-то воспринимаются с меньшим сопротивлением. Разумеется, свойством обладать русским названием латинские буквы ничем в принципе не отличаются от других знаков – тире, дефиса, тильды, греческих букв, русских букв, букв кириллицы.

Для немецкого, французского и многих других языков буквы латинского алфавита являются родными, так как специальных названий, отличающихся от французских и немецких, нет. В русском же языке многие названия латинских букв такие же (на самом деле, конечно, почти такие же), как во французском и немецком.

Русские названия для букв A, B, D, F, I, K, M, N, O, P, R, S, T, X такие же, как в немецком и французском языках. Русские названия для букв C, J, Q, U такие же, как в немецком (но не во французском) языке. Русские названия для букв G, H, L, V, W такие же, как во французском (но не в немецком) языке. Русское название для Y такое же, как во французском языке, но с переносом ударения на первый слог, русское название для Z такое же, как во французском, но с оглушением последнего согласного. Название для E чисто русское.

Лист определений «Латинские буквы»

 Конечно, мы понимаем, что усвоение латинского алфавита не пройдет так же гладко, как усвоение русского. Действительно, основная масса детей неплохо ориентируется в русских буквах еще при поступлении в школу – знает названия, может написать, прочесть, имеет представление об алфавитном порядке русских букв. Поэтому соответствующие листы определений 1 класса («Русские буквы и цифры», «Русская алфавитная цепочка») носили скорее характер обобщения и систематизации уже известного детям материала.  С латинским алфавитом ситуация иная, в целом мы не рассчитываем на то, что дети хорошо знакомы с латинским алфавитом. Однако мы считаем важным, провести это знакомство как можно раньше по нескольким причинам. Во-первых, как буквы кириллицы составляют основу русского алфавита и соответственно письменности, так буквы латиницы являются основой письменности многих иностранных языков. Таким образом, знакомство с латиницей закладывает у детей основы лингвистической культуры и языковой толерантности. Во-вторых, латинские буквы широко употребляются во многих науках, включая информатику и математику. В-третьих, латинские буквы часто употребляются в разных сферах практической деятельности человека.

Поскольку мы планируем на этом листе определений первое знакомство с латинскими буквами, мы предлагаем вам взять на вооружение следующие основные подходы к данной теме. Во-первых, не стоит рассчитывать на то, что дети после этого урока запомнят (или тем более, заучат) все буквы латинского алфавита с их названиям и указанием алфавитного порядка. Поэтому чаще побуждайте детей в случае затруднения обращаться к листу определений. Это желание у ребенка надо приветствовать во всех темах, а здесь без этого не обойтись. Во-вторых, как и русские буквы, латинские буквы нас интересуют в первую очередь как символы, из которых можно составлять в дальнейшем структуры. Поэтому основное умение, которое мы хотим сформировать в данной теме – умение выделять латинские буквы и отличать их от русских. При этом надо иметь в виду, что эта задача не всегда разрешима в отрыве от контекста (языкового или другого). Так некоторые буквы (символы) встречаются только в русском алфавите (Б, Ж, Щ и т. д.), их можно в уверенностью назвать русскими буквами. Некоторые буквы (символы) встречаются только в латинском алфавите (Q, W, R, Y и т. д.), их можно с уверенностью назвать латинскими буквами. Однако имеется ряд символов, которые есть и в русском и в латинском алфавите, поэтому их можно считать как русскими, так и латинскими буквами. Уточнить это обычно удается, учитывая контекст, в котором эта буква встречается. При этом задача, как правило, переходит в разряд лингвистических. Этот довольно тонкий вопрос лучше не обсуждать сразу, а обратиться к нему при решении задач.

Еще одна (долгосрочная) цель этого урока – сформировать у ребят умение пользоваться латинской алфавитной линейкой (так же, как они сейчас учатся пользоваться русской). Данную задачу мы не планируем полностью решить на этом и ближайших уроках, скорее это задача будущего. В настоящий момент дети всегда смогут заглянуть в латинскую алфавитную цепочку. Ну и наконец, нам бы очень хотелось, чтобы дети научились правильно называть латинские буквы. Это умение тоже надо формировать постепенно, побуждая детей в случае ошибки обратиться к листу определений.

Также мы обращаем внимание детей на этом листе определений на то, что латинские буквы (как и русские) могут быть строчными и прописными. Детям это пригодится при решении некоторых задач.

Мы не советуем вам отводить на знакомство с листом определений «Латинский алфавит» слишком много времени. К этому листу определений правильней всего относиться как к справочному материалу, к которому дети всегда смогут обратиться при решении задач.

Решение задач из учебника

Задача 144. Эта задача на усвоение русских названий латинских букв. При этом, конечно, детям разрешается заглядывать на лист определений «Латинский алфавит». Главное здесь – не перепутать латинские буквы с русскими буквами, имеющими то же написание.

Задача 145.  Задача на различение русских и латинских букв. Как мы говорили, это различение не всегда ведет к однозначному результату, поскольку есть символы, которые в равной степени можно считать буквами, как русского, так и латинского алфавита. Однако, в данной задаче мы пока не хотим обсуждать с ребятами этот тонкий вопрос. Поэтому мы выбрали одинаковые русские буквы из числа тех, которых нет в латинском алфавите и латинские из числа тех, которых нет в русском алфавите. Тем не менее, здесь есть другие ловушки, в которые может попасться невнимательный ребенок. Так в русском и латинском алфавитах есть буквы довольно похожие, но, тем не менее, разные. Мы не предлагаем детям отличить русскую К от латинской K – это различие слишком тонко. Но вот разобраться с буквами Г и L, И и N вполне посильная задача.

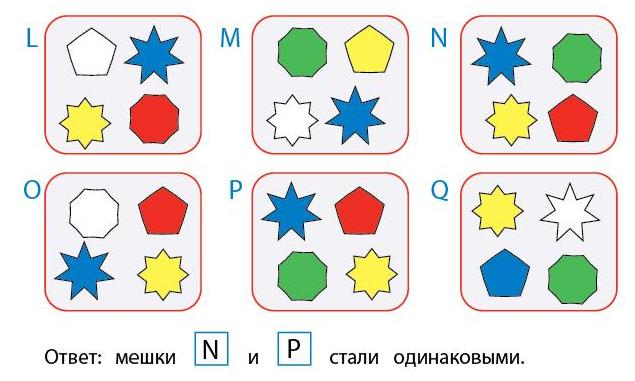
Задача 146. Из условия задачи следует, что в каждом мешке должно стать 4 монеты. Анализируя мешки, делаем вывод, что в каждом мешке должна быть монета в 5 рублей, монета в 2 рубля, монета в 1 рубль. Что касается четвертой монеты в мешках, она может быть любой

Задача 147. Задача на алфавитный порядок латинских букв. Ее большинство детей будут решать с опорой на алфавитную цепочку на листе определений. Если вы будете проводить фронтальную проверку, проследите за тем, чтобы дети правильно называли латинские буквы.

Задача 148. Необязательная. После введения латинских букв, мы постепенно будем начинать использовать в наших задачах английские слова (и слова других языков), ведь английский алфавит использует латиницу. Среди данных утверждений имеется только два истинных – первое и последнее (остальные утверждения ложны). Однако, большинство детей наверняка напишут букву Н в окне около последнего утверждения. Вряд ли хоть кто-нибудь в вашем классе знает, что Гранд Сентрал – это вокзал. Впрочем, вы можете рассказать детям перед решением этой задачи то, что написано ниже о названиях станций.

Здесь, как и в других подобных случаях, полезно (хотя и необязательно) уметь произносить названия объектов, о которых идет речь. В данном случае эти объекты – названия станций одной из линий метро в центральной части Нью-Йорка – на острове Манхеттен. Эта линия проходит вдоль всего острова, с юга на север. Для тех из вас, кто учил английский язык, произносить названия станций будет нетрудно. Для других приводим примерное произношение. (Конечно, русские звуки отличаются от английских, но, честно говоря, в Нью-Йорке большинство людей говорят на далеко не безупречном языке.) Итак, названия станций читаются примерно так:

Боулинг Грин

Кэнэл (речь идет о Кэнэл стрит, а кэнэл по-русски – это «канал»).

Спринг (опять-таки Спринг стрит, спринг значит и «весна», и «пружина», и «источник, ключ», интересно, правда?). Название улицы связано, скорее всего, с последним значением.

Дальше идут улицы с номерами. С таким обозначением улиц мы встречаемся и в Москве, и в других городах (3-я улица Восьмого марта до сих пор существует в Москве, в районе метро Аэропорт). Но американцы развили эту идею до высокого уровня. Например, в Вашингтоне, как и в Нью-Йорке, имеется прямоугольная сеть улиц, при этом поперечные улицы имеют номера, а продольные называются разными именами, но первые буквы этих имен идут по алфавиту. Представьте себе, как это было бы в Москве: Аральская, Балтийская, Вологодская, Гомельская, Дубнинская; или Афанасьевская, Борисовская, Владимирская, Георгиевская, Давыдовская и т. д.

Хантер колледж (это действительно колледж и довольно известный). Колледж частный, как и большая часть высших учебных заведений в Америке, в нем, как и в колледжах и университетах, принадлежащих штату, за обучение надо платить. Хантер значит «охотник», но в данном случае речь идет, скорее всего, о конкретном человеке с такой фамилией.

Бликер

Гранд Сентрал – это Главный вокзал (американцы мало ездят на поездах, больше на автомобилях и самолетах, но все же вокзалы в некоторых городах еще существуют, поезда достаточно комфортабельны и дешевы, поездка на поезде из Нью-Йорка в Вашингтон не такая уж экзотика).

Задача 149. В данном случае даны две одномерные таблицы для мешка (по форме и по цвету фигурок). Дополнительным условием является набор фигурок на листе вырезания (из которых детям придется выбирать). Это ограничение представлено неявно, однако его придется соблюдать волей неволей. Так лимоны на листе вырезания только желтые, поэтому детям придется в любом случае наклеить в мешок их. Кроме того видим, что зеленые на листе вырезания только груши, а синие – только сливы. Поэтому придется наклеить в мешок две синие сливы и две зеленые груши. После этого у нас появляется выбор – нам нужно поместить в мешок 3 красных фигурки и 2 желтых, причем среди них должно быть 3 яблока, 1 груша и 1 слива. Поскольку и яблоки, и груши, и сливы у нас есть и красные, и желтые, это можно сделать по-разному.

Задача 150. Здесь ребята ищут слова, в которых известна первая буква. Это значительно уменьшает перебор. Итак, находим в Словаре все слова на П и проверяем их последние  буквы. В результате отыскиваются два подходящих слова – ПЕРВЫЙ и ПЯТЫЙ.

Задача 151. Необязательная. Первое и второе утверждения позволяют выделить отрезок цепочки слов Словаря, на котором есть смысл анализировать слова более тщательно. Это отрезок слов от слова ДЕВЯТНАДЦАТЬ до слова ЖЕЛТЫЙ.

Ответ: ДЕРЕВНЯ, ЕДИНИЦА, ЕЖЕВИКА, ЖАРА, ЖЕЛЕЗО.

Задача 152. Необязательная. Многие дети будут, скорее всего, заглядывать в лист определений на странице 65. Из-за этого у кого-то из детей уйдет на эту задачу достаточно много времени. Тем не менее, не нужно никого торопить и уж тем более подсказывать – в процессе именно такой деятельности дети запомнят латинскую алфавитную цепочку лучше всего.

Надеемся, все дети поймут формулировку «соедини буквы в алфавитном порядке». Дети уже решали похожую задачу с русскими буквами. Это означает, что надо А соединить с В, затем В – с буквой С и т. д. до буквы Z. Чтобы рисунок получился аккуратным, лучше использовать при соединении точек линейку. Что касается проверки, здесь не обязательно проводить ее очень скрупулезно. Действительно, при правильном соединении точек на картинке появится парусник.

Задача 153. Если кто-то из ребят затрудняется с решением этой задачи, попросите его отметить на латинской алфавитной линейке, приведенной справа, буквы V и Q. Все искомые буквы будут находиться на линейке между ними.

Задача 154. Можно задать детям перед решением задачи вопрос о том, как определить истинность первого и второго утверждений, не заглядывая в Словарь. Можно не давать на него ответ сразу – достаточно, если сильные и средние дети над этим задумаются. Конечно, не заглядывая в Словарь можно определить истинность таких утверждений только в том случае, если мы уверены, что слова, о которых идет речь в утверждении в Словаре есть. В противном случае утверждение будет бессмысленным. Сразу скажем, что бессмысленные утверждения в задачах подобных данной вообще не встречаются. Тем не менее, если ребенок может определить истинность утверждений, не заглядывая в Словарь, в конце он все равно должен заглянуть в Словарь, чтобы проверить свое решение (и заодно убедиться, что ни одно утверждение не теряет смысла).  Среди данных утверждений одно ложно, а остальные – истинны.

Задача 155. Здесь в одном из мешков все фигурки уже раскрашены, а раскрасить мы должны лишь одну фигурку. Отсюда делаем вывод – один из одинаковых мешков будет тот, в котором все фигурки уже раскрашены. Теперь остается сравнить этот мешок со всеми остальными и найти второй мешок пары.

Задача 156. В ходе решения этой задачи ребята могут убедиться в том, что при ссыпании мешка с пустым мешком получается такой же мешок.

Задача 157 аналогична задаче 150 (см. комментарий к задаче 150).В результате отыскиваются два подходящих слова – КЛАСС и КРОВАТЬ.

Задача 158. Необязательная. Аналогичные задачи ребятам уже встречались (см. комментарий к задаче 87).

Задача 159. Необязательная. На примере этой задачи ребята могут повторить случаи бессмысленности утверждений. Так, среди данного набора есть слово, в котором буквы «О» вообще нет – слово ФИНАЛ. Кроме того, есть слова, в которых буква «О» не одна, например, слово ФОРТОЧКА и ФОТО. В общей сложности отмеченными оказываются 3 слова.

Компьютерный урок «Латинский алфавит»

Решение задач 157 – 167

Задача 157. В этой задаче ребята закрепляют латинскую алфавитную цепочку.

Задача 158. Как мы уже говорили, если дети изучают английский (или другой иностранный) язык со 2 класса, то с названиями латинских букв может возникать путаница – дети называют их в курсе так, как они называют соответствующие английские буквы. Поэтому в данной задаче нужно специально обратить внимание детей на то, что решение задачи (как всегда!) должно заканчиваться проверкой. После того, как учащийся заполнил все окна, он должен открыть второй экран листа определений и сравнить названия данных букв с названиями, которые там приведены.

Задача 159. По ходу решения этой задачи детям приходится не только искать одинаковые буквы, но и отделять латинские буквы от цифр и русских букв. Если для кого-то из ребят это окажется трудно, попросите его сначала вычеркнуть в наборе все русские буквы и цифры. После этого в случае затруднений можно предложить учащемуся провести полный перебор всех латинских букв с использованием пометок.

Задача 160. Здесь детям нужно определить значения истинности утверждений о латинской алфавитной цепочке. Как и в компьютерной задаче 157, большинство ребят будут решать эту задачу с опорой на латинский алфавит. Некоторые дети в этой задаче будут путать латинские буквы с русскими, поэтому пометят первое утверждение как истинное, а второе – как ложное. Особое внимание стоит обратить на утверждения, не имеющие смысла. Таких утверждений здесь два: третье (поскольку в латинском алфавите нет букв Ш и Ц) и предпоследнее (так как в латинском алфавите нет буквы следующей после Z).

Задача 161. Поскольку букв много, лучше использовать по ходу перебора пометки. Если для буквы истинны оба утверждения, стоит сразу пометить ее красной галочкой. Если – хотя бы одно утверждение ложно, букву можно сразу вычеркнуть (чтобы не возвращаться к буквам, которые уже просмотрены). Наибольшие проблемы, скорее всего, возникнут с буквами U и F. Чтобы показать, что для буквы F второе утверждение ложно, можно перейти на примеры, близкие ребенку. Например, спросить его можно ли сказать, что он проснулся позже, чем проснулся или что звонок на первый урок прозвенел позже, чем звонок на первый урок.

Задача 162. Как и в компьютерной задаче 148, первая буква искомого слова неизвестна, но известно, что это одна из букв данного мешка и что она идет в алфавитной цепочке раньше буквы Д. Значит, искомое слово может начинаться на буквы: А, Б или Г. Теперь можно перебрать все слова на данные буквы. Перебор можно существенно сократить, если использовать число букв данного слова. Так в Словаре есть лишь одно слово из 7 букв (АВТОБУС), которое не подходит по набору букв.

Задача 163. В данном случае по условию фигурки разрешено переставлять только в цепочке Т, поэтому фигурки в цепочке У запрещены для перемещения.

Задача 164. Задача на выделение из набора латинских и русских букв. Обратите внимание, среди данного набора имеются буквы, которые есть как в русском, так и в латинском алфавите. Поэтому от ребенка требуется соблюдать последовательность действий, описанную в задаче. Сначала выделить все русские буквы – буквы, которые есть в русском алфавите, и положить их в мешок Р. В том числе в мешок Р попадут естественно и те буквы, которые являются как русскими, так и латинскими: А, В, Е, К. Теперь из оставшихся символов нужно выделить латинские буквы и положить в мешок Л. Как видите, при такой формулировке в мешке Л окажутся только те латинские буквы, которых нет в русском алфавите.

Задача 165. Подходящих решений в этой задаче достаточно много. При этом можно начинать строить цепочку с любого утверждения почти как угодно. Например, можно сначала поставить фотоаппарат позже лодки, а потом на любое свободное место в цепочке поставить связку ключей, а за ней – уточку. Можно поступить и наоборот. Компьютерная «лапка» дает возможность по ходу дела передвигать фигурки, поэтому не помогайте детям чрезмерно. Сильным детям будет достаточно указать на наличие ошибки, а слабым – показать несоответствие цепочки одному из утверждений.

Задача 166. Аналогичная задача в курсе ребятам уже встречалась (см. комментарии к компьютерной задаче 103 урока 10).

Задача 167. Необязательная. Вынем все деньги из кошельков и будем раскладывать их сразу во все кошельки поровну, стараясь при этом использовать монеты одинакового достоинства (если такое возможно). Начинать лучше при этом с крупных монет. Так у нас имеется 7 пятирублевых монет, значит можно положить в каждый кошелек по одной такой монете и одна еще останется. Положим ее в один из кошельков и положим во все остальные кошельки по 5 рублей, используя двухрублевые и рублевые монеты. У нас это получается. Теперь оставшиеся монеты раскладываем по кошелькам поровну, начиная с двухрублевых монет. В какой-то момент монеты заканчиваются, и оказывается, что суммы денег во всех кошельках одинаковые.

Проект «Римские цифры»

О проекте

Цель данного проекта — познакомить детей с римской нумерацией. Данный проект играет в курсе общеразвивающую, пропедевтическую функцию. Он не связан напрямую с изучаемым материалом, но играет очень важную роль в формировании общей осведомлённости ребёнка, его знакомстве с окружающим миром. Действительно, детям довольно часто приходится сталкиваться с римской нумерацией. Так, римскими цифрами принято нумеровать века. Часто так нумеруют главы книг, иногда такие числа можно увидеть на циферблате часов и пр. Например, в тетради проектов страницы вкладыша пронумерованы римскими цифрами, чтобы дети с одной стороны не перепутали с основными страницами тетради (где помещены задания) и, с другой стороны, можно было точно указать нужную страницу.

Данный проект выполняется в основном индивидуально. Для решения трудных задач вы можете объединять ребят в пары или группы по 3—4 человека. Форма работы с отдельными задачами определяется учителем.

Материалы к данному проекту можно найти в тетради проектов на с. 14—15. Текст в условии задачи 12 на с. 14 не является листом определений в том смысле, который принят в курсе, то есть изучение этого текста не является необходимым условием решения задач. Именно поэтому текст не выделен специальной рамкой. Этот текст приводится для повышения эрудиции и общей осведомлённости ребёнка. Поэтому формы работы с данным текстом также выбирает учитель. Например, дети могут с ним работать как с обычным листом определений. Также его можно прочитать, сделав основой для разговора о римской нумерации (в этом проекте вполне допустимо фронтальное обсуждение вопроса). Если вы хотите сэкономить время для решения задач, можно попросить детей прочитать текст дома.

Решение задач 12 – 19 из тетради проектов

Задача 12. Это одна из немногих задач курса, где использовано слово «догадайся». В учебнике таких задач не встретишь, поскольку работа в рамках явно введённых правил игры практически исключает подобные формулировки. В проектах, где формы работы более свободные, а результаты работы не настолько жёстко регламентированные, такие формулировки принципиально возможны. Часть детей, возможно, уже немного знакома с римской нумерацией, для них данная задача будет полезным упражнением на закрепление своих знаний. Кто-то из детей заметит, что страницы в тетради проектов пронумерованы римскими цифрами, и догадается использовать это для решения. Остальных ребят формулировка данной задачи приглашает к поиску закономерности на основе сравнения арабских цифр, с которыми дети уже знакомы, с римскими цифрами. Конечно, выдвигаемые учащимися гипотезы будут не всегда верными, будут часто основаны на ошибочных аналогиях. Так, из таблицы видно, что число 1 записывается одной палочкой, число 2 — двумя палочками, число 3 — тремя. Отсюда кто-то из детей может сделать вывод, что каждое число в римской нумерации записывается соответствующим числом палочек. Следует обратить внимание учащихся на то, что число 5 записывается не пятью палочками (как это можно было бы ожидать), а галочкой. При этом число 4 записывается галочкой и палочкой слева, а число 7 — галочкой и двумя палочками справа. Тут кто-то из ребят, наверняка, вспомнит, что число 4 на 1 меньше пяти, а 7 — на 2 больше. Это и даёт ключ к записи числа 6. Теперь переходим к записи числа 8. Насчёт него у ребят может возникнуть спор — основная масса ребят запишет его галочкой и тремя палочками справа (поскольку 8 = 5 + 3), но возможно некоторые запишут 8 крестиком и двумя палочками слева (поскольку 8 = 10 – 2). Поскольку никаких явных договорённостей в этом проекте не вводилось, вы можете уладить спор двумя способами. Либо обратить внимание ребят на то, что ни в одном числе нет больше одной палочки слева от знака V и X (можно ввести эту договорённость явно), либо открыть книгу, где использована римская нумерация, и попросить детей проверить свой ответ.

Задача 13. Из курса математики дети знают, что любое число второго десятка можно представить в виде суммы числа 10 и некоторого числа первого десятка. Именно этот факт и используется в римской нумерации чисел второго десятка. Поэтому, если к числам первого десятка, которые дети получили в задаче 12, приписать слева крестик, обозначающий десяток, получатся числа второго десятка. Не все дети догадаются до этого сразу, с некоторыми вам придётся обсудить закономерности построения чисел.

Задача 14. В этой задаче обсуждается нумерация чисел третьего десятка. Работа ведётся так же, как в предыдущих задачах.

Задача 15. Задача, обратная задачам 12—14. Здесь нужно записать арабскими цифрами числа, записанные римскими. Проще всего это сделать, опираясь на заполненные в задачах 12—14 таблицы. Если кто-то из ребят будет решать задачу без опоры (в уме) и допустит в ней ошибки, можно вернуть их к решению предыдущих задач или просто дать книгу, в которой использована римская нумерация (например, вкладыш тетради проектов), и попросить пронумеровать её части (страницы, главы, разделы) с помощью арабских цифр.

Задача 16. Эта задача посвящена римской нумерации круглых чисел (чисел, оканчивающихся на цифру 0). Как записываются римскими цифрами числа 10, 20, 30, дети уже знают. Запись остальных чисел ребятам предлагается придумать самостоятельно, используя то, что знак L используется для обозначения числа 50. Проще всего при этом построить аналогию с нумерацией чисел от 1 до 8. При этом знак Х будет играть роль I, а знак L будет играть роль V.

Задачи 17 и 18. Необязательные. Эти задачи посвящены римской нумерации чисел от 40 до 89. При нумерации таких чисел используется знак L. При решении этих задач проще всего использовать таблицы из задач 16 и 12, принимая во внимание, что любое двузначное число можно представить в виде суммы круглого числа и числа первого десятка.

Задача 19. Необязательная. В отличие от римской нумерации запись чисел знаками Майя не будет знакома, скорее всего, никому из ребят. Поэтому в этой задаче все дети будут в равном положении — всем придётся искать закономерность и строить гипотезы. Так, нетрудно заметить, что до числа 4 каждое число обозначается соответствующим числом точек, а число 5 — горизонтальной палочкой. Это означает, что в нумерации Майя используется счёт с выделением пятёрок. Этот вывод в частотности подтверждает то, что число 10 записывается двумя палочками. Теперь нетрудно записать пропущенные числа. Например, 7 = 5 + 2, значит, число семь записывается палочкой и двумя точками, число 15 = 10 + 5 (или 5 + 5 + 5), значит, число 15 записывается тремя палочками.

Компьютерный проект «Римские цифры»

Лист определений «Римские цифры»

Данный лист определений не совсем похож на остальные листы определений, содержащиеся в курсе. Обычно на листах определений мы приводим только ту информацию, которая необходима детям для решения задач. Здесь лист определений содержит разные виды информации, в частности сведения общеразвивающего характера (например, когда, кем и откуда была принесена та или иная система записи чисел). Эти сведения не важны для прохождения материала курса и решения задач, но детям они могут быть полезны с точки зрения общей эрудиции. Информация, которая связана с арабской нумерацией, детям, скорей всего, известна из курса математики, ее мы приводим просто для полноты картины. Вообще, с точки зрения решения задач детям важно разобрать только вторую часть второго экрана листа определений, то есть примеры римских записей различных чисел от 1 до 20. Именно эти примеры позволяют детям сформулировать определенные закономерности римской записи чисел, которые позволят им в задачах переходить от римской записи к арабской и наоборот. Нужно ли обращать внимание ребят на отличие данного листа определений и нужно ли предлагать какие-то особенные формы работы с этим листом определений в каждом конкретном классе, решает учитель.

Решение задач 168 – 172 из проекта «Римские цифры»

Задача 168. Часть детей, возможно, уже немного знакома с римской нумерацией, для них данная задача будет полезным упражнением на закрепление знаний. Остальных ребят формулировка данной задачи приглашает еще раз обратиться ко второму экрану листа определений с целью поиска закономерности построения римской записи чисел на основе сравнения чисел в арабской и римской записи. Конечно, выдвигаемые учащимися гипотезы будут не всегда верными, основанными на ошибочных аналогиях. Так, на листе определений указано, что число 1 записывается одной палочкой, а число 3 – тремя. Отсюда кто-то из детей может сделать вывод, что каждое число в римской нумерации записывается соответствующим числом палочек. Следует обратить внимание учащихся на то, что пять записывается не пятью палочками (как это можно было бы ожидать), а галочкой. При этом 4 записывается галочкой и палочкой слева, а семь – галочкой и двумя палочками справа. Тут кто-то из ребят, наверняка, вспомнит, что число 4 на 1 меньше пяти, а 7 – на два больше. Это объясняет построение римской записи числа 9 (на основании равенства 9 = 10 - 1) и дает ключ к записи числа 6 на основании равенства 6 = 5 + 1. Теперь переходим к записи числа 8. Насчет этого числа у ребят может возникнуть спор – основная масса ребят запишет его галочкой и тремя палочками справа (поскольку 8 = 5 + 3), но, возможно, некоторые запишут 8 крестиком и двумя палочками слева (поскольку 8 = 10 - 2). Поскольку никаких явных договоренностей об этом в проекте не вводилось, вы можете уладить спор двумя способами. Либо обратить внимание ребят на то, что ни в одном числе нет больше одной палочки слева от пятерки или десятка (можно ввести эту договоренность явно), либо проанализировать римскую запись числа 18.

Теперь перейдем к нумерации чисел от 10 до 20. Число 10 обозначается латинской буквой Х. К настоящему моменту дети уже знают, что любое число второго десятка можно представить в виде суммы числа 10 и некоторого числа первого десятка. Именно этот факт и используется в римской нумерации чисел второго десятка. Поэтому если к числам первого десятка приписать слева крестик, обозначающий десяток, получатся числа второго десятка. Не все дети догадаются до этого сразу, с некоторыми вам придется обсудить закономерности построения чисел. Лучше всего начать со сравнения записи чисел 4 и 14 с листа определений.

Задача 169. Эта задача посвящена римской записи чисел от 21 до 39. Если учащийся затрудняется с решением этой задачи или делает ошибки, обсудите вместе данные в задаче примеры с опорой на разрядный состав чисел. Например, рассмотрим римскую запись числа 29. В числе 29 два десятка и 9 единиц. Римская запись числа 29 также содержит обозначения двух десятков (два крестика), а затем – запись числа 9. Таким образом, в римской нумерации, как и в арабской, сначала надо записать десятки числа, только не количеством, а перечислить все десятки по одному (обозначив каждый символом Х), а затем записать число единиц так, как это было сделано на листе определений и в задаче 168.

Задача 170. Эта задача по типу – обратная задачам 168 и 169, здесь надо числа в римской записи перевести в запись арабскими цифрами. Как и в задачах 168 и 169, при возникновении затруднений нужно опираться на разрядный состав числа. Но если в арабской записи дети легко разбивают число на десятки и единицы, то в римской записи дети этому только учатся. При необходимости учащемуся стоит объяснить, что десятки в римской записи расположены подряд, в начале числа. Они заканчиваются там, где в записи встречается первый другой символ (не крестик). Например, рассмотрим второе число во втором столбце. В начале его стоят подряд 3 крестика до галочки (первого не крестика). Это значит, что в данном числе имеется 3 десятка, а с галочки начинается запись числа единиц.

Задача 171. Эта задача посвящена римской нумерации чисел от 40 до 89. Данная задача несколько сложнее предыдущих. Мало кто из детей встречался с такими большими числами в римской записи, поэтому использование знака «L» придется по-настоящему прорабатывать (никакой привычки на этот счет у детей нет). Если предыдущие задачи дети решали с трудом, лучше сначала подождать, пока у ребят в головах уляжется нумерация чисел от 1 до 39, и решить задачи 171 и 172 на следующих уроках.

Если вы спросите до решения данной задачи, как дети бы записали число 45, то продолжая логику предыдущей задачи, ребята, скорее всего, предложат вам запись ХХХХV. В этом случае стоит обратить внимание учащихся на то, что такая запись по такому принципу может быть чрезмерно длинной. Так, для числа 88 нам пришлось бы рисовать 8 крестиков – при этом легко сбиться. Поэтому для римской записи чисел от 40 до 89 используется знак L, который обозначает 50. В случае затруднений стоит сначала обсудить с ребенком нумерацию всех круглых чисел от 40 до 80. Лучше всего выписать все соответствующие записи, чтобы в дальнейшем использовать их как справочный материал. Кроме того, для решения этой задачи, как и предыдущей, учащимся потребуется умение отделять в римской записи десятки от единиц. В числах до 39 десятки всегда обозначались крестиками, теперь десятки обозначаются знаками L и Х. Таким образом, десятки чисел от 10 до 89 заканчиваются там, где встречается первый другой символ (не L и не Х). Начиная с этого символа, идет запись единиц числа.

Задача 172. Это наиболее сложная из предложенных в этом проекте задач, поскольку здесь надо использовать знания о нумерации всех чисел, которые обсуждались: чисел первого и второго десятка, чисел от 20 до 39, чисел от 40 до 89.

Решение задачи урока 4  для «Водолея»

Задача 1 (Водолей). Большинство детей по-прежнему продолжают решать подобные задачи методом проб и ошибок, выполняя различные команды с данными емкостями и глядя на то, что получилось (по ходу лучше записывать все новые объемы, которые удалось получить, чтобы не повторять одни и те же варианты проб). Кто-то из ребят уже пробует использовать в таких задачах арифметические соображения. Например, ясно, что если два раза налить из полного 12-литрового сосуда в пятилитровый, то в 12-литров останется 2 литра воды. 4 литра можно получить, налив 2 раза по 2 литра.