Информатика. 2 класс Демо+методичка

Уроки 21–22. «Мешок бусин цепочки»

Мешок бусин цепочки – понятие несложное, но для нас достаточно важное. Оно устанавливает связь между понятиями цепочка и мешок. Если взять цепочку и лишить ее порядка (ссыпать элементы в кучку), получится мешок элементов. При этом для каждой цепочки существует ровно один мешок ее элементов. Если взять мешок и установить между его элементами какой-нибудь порядок, получится, конечно же, цепочка. Это цепочка, для которой данный мешок – мешок ее элементов. Однако существует много таких цепочек. На листе определений приведен подобный пример с мешком букв Щ.

На понятии мешок бусин цепочки базируется большой пласт комбинаторно-языковых и других задач. Операция ссыпания бусин цепочки в мешок является типичным примером операции гомоморфизма, играющей важную роль в современной алгебре и в математике вообще.

Решение задач из учебника

Задача 130. С содержательной точки зрения эта задача не сложная – для ее решения достаточно понимать, что такое мешок бусин цепочки. Действительно, порядок бусин в цепочке здесь не играет существенной роли, поэтому можно лишь стремиться к тому, чтобы два набора бусин (в цепочке и в мешке) были одинаковыми. Стратегия решения здесь может состоять в том, чтобы провести полный перебор (используя пометки) раскрашенных бусин сначала в цепочке, а затем в мешке. Ни для одной раскрашенной бусины в цепочке  Ю в мешке Ж нет такой же, поэтому придется для каждой бусины цепочки раскрашивать ей пару в мешке.

Задача 131. Здесь необходим полный перебор слов и сопоставление их с мешком букв. Однако, можно немного упростить себе работу и делать перебор не так уж тщательно, если заметить некоторые особенности слов и мешка И. Во-первых, в мешке ровно 6 букв, значит все слова, в которых другое число букв можно сразу вычеркивать. В результате у нас остается лишь два слова: ШАШЛЫК и ЛАНДЫШ. Их нужно сопоставить с мешком И более тщательно. В результате получаем, что условию задачи соответствует лишь одно слово – ЛАНДЫШ.

Задача 132. Построить все цепочки, соответствующие одному мешку бусин – непростая комбинаторная задача. Здесь, однако, можно обойтись и без перебора, ведь разных цепочек нужно построить всего три. Самый простой способ сделать это – поставить на первые места в этих цепочках три разные бусины из мешка Б, тогда оставшиеся бусины в цепочках можно будет расставлять как угодно.

Задача 133. Достаточно объемная задача, требующая внимательности и определенного уровня техники. Можно немного схитрить и вести перебор не по числам, а по мешкам, поскольку их меньше. Кроме того, можно при этом использовать особенности чисел в мешках. Например, в первом мешке нет цифры 2, а во всех остальных мешках она есть, значит можно соединить с первым мешком все числа, в которых нет двойки. Во втором мешке нет цифры 4, а во всех оставшихся двух мешках (кроме первого, с которым мы уже соединили все его числа) четверка есть. Значит, соединяем все свободные числа без четверки со вторым мешком. Теперь осталось распределить все оставшиеся числа по двум оставшимся мешкам.

Задача 134. Необязательная. Знакомая ребятам, но технически непростая задача. При возникновении проблем стоит придумать вместе с учащимся какой-то способ перебора и учета просмотренных букв. Один из вариантов – брать каждую букву и вычеркивать все такие же буквы, а рядом с ней ставить число таких же букв.

Задача 135. Здесь третье утверждение – истинно, остальные – ложные.

Задача 136. Необязательная. Вы наверняка заметите, что кто-то из детей решит эту задачу почти мгновенно, а кто-то сидит над первым заданием довольно долго. Причина в том, что единственный формальный путь поиска нужного нам слова – полный перебор всех слов, для которых Ю мешок букв, слишком долог. Зато случайно наткнуться на решение здесь можно очень быстро. Поэтому если вы видите, что кто-то из ребят испытывает в этой задаче серьезные затруднения, подскажите ему поискать слова, начинающиеся на букву Т. В таком случае перебор будет существенно меньше. Второе задание этой задачи имеет, конечно, много решений.

Задача 137. Наиболее простой способ решения этой и подобных задач – вырезать из листа вырезания всех бабочек, которые лежат в мешке С и перекладывать их в цепочке Ч или просто на парте до тех пор, пока все данные утверждения не станут истинными. Третью фигурку с конца – синюю бабочку можно поставить на место сразу. Затем можно поставить за ней зеленую бабочку. Теперь у нас остались лишь два свободных места в цепочке, стоящих подряд – первое и второе. На них мы и ставим желтую и коричневую бабочку. После этого красную бабочку помещаем на оставшееся свободным место. Получаем решение: желтая бабочка – коричневая бабочка – синяя бабочка – зеленая бабочка – красная бабочка.

Задача 138. Данная задача аналогична задаче 131. В мешке Щ 8 букв, значит, подойдут только те слова, в которых 8 букв, а таких в нашем наборе шесть. Довольно быстро убеждаемся, что из этих шести слов подходит три  – ПАСЕЧНИК, ПЕСЧАНИК, ПЕСЧИНКА.

Задача 139. Необязательная. Данная задача имеет несколько решений, поэтому найти хотя бы одно подходящее решение не так уж сложно. Слабому ученику в случае затруднений лучше посоветовать собрать нужный мешок бусин и перекладывать их на столе, строя цепочку методом проб и ошибок.

Задача 140. Заметим, что одинаковых мешков здесь просто нет. Поэтому данная задача в значительной степени арифметическая. Наиболее простой способ ее решения – посчитать вначале сумму денег в каждом мешке и затем среди этих сумм найти две одинаковые.

Задача 141. Знакомая детям задача на поиск слов в Словаре по образцу, предназначенная преимущественно для средних и слабых учащихся. Сильным ученикам такую задачу будет решать, скорее всего, уже не интересно.

Задача 142. Задача аналогична задаче 125, только инструкция здесь несколько длиннее (см. комментарий к задаче 125).

Задача 143. Необязательная. Это довольно сложная задача, близкая к комбинаторным. Действительно, здесь речь идет о поиске всех комбинаций трех клеток, раскрашенных в один из двух цветов. На самом деле таких комбинаций, то есть различных фигурок, можно построить ровно 8. Ясно, что первая клетка (верхнего ряда) может быть раскрашена в один из двух цветов, значит, у нас есть 2 варианта раскраски верхнего ряда и даже двух верхних рядов (поскольку во втором ряду мы ничего не раскрашиваем). Если присоединить сюда еще и третий ряд, то вариантов станет больше, ведь в каждом из двух вариантов раскраски верхней клетки, можно раскрасить клетку в третьем ряду снова в два цвета. Таким образом, существует 4 варианта раскраски первых трех рядов фигурок. При каждом из этих вариантов, клетку нижнего ряда можно раскрасить в один из двух цветов, поэтому вариантов раскраски фигурок в задаче существует ровно 8. У нас фигурок 6, значит, вариантов нам хватит – можно сделать все 6 фигурок разными. Подобные рассуждения мы приводим не для того, чтобы их повторяли дети. Просто мы хотим показать, что задача действительно по сути комбинаторная и здесь мы потихоньку ведем пропедевтику довольно сложных математических вопросов. Однако, дети будут действовать иначе, скорее всего, методом проб и ошибок. Например, раскрасят первую фигурку наугад. Теперь вторую фигурку надо раскрасить так, чтобы они с первой оказались разными. Вообще-то для этого достаточно раскрасить хотя бы один квадратик в другой цвет, но можно поступить и по-другому. Теперь третью фигурку надо раскрасить так, чтобы она не совпадала ни с первой, ни со второй фигуркой и т. д. Если вы видите, что в решении допущена ошибка, достаточно указать ребенку пару одинаковых фигурок, а как исправить раскраску, пусть подумает сам.

Компьютерный урок  «Мешок бусин цепочки», 1 часть

Решение задач 143 – 149

Задача 143. Здесь дети имеют возможность сами проделать все действия, которые на листе определений описывались словами. В этом и заключается крупное преимущество работы ребенка в нашей компьютерной среде. Так в этой задаче учащийся сначала сам складывает лапкой (ссыпает) бусины в мешок, а затем снова собирает из них цепочку. Конечно, в процессе такой явной сборки ребенок убедится, что цепочки, построенные из бусин одного мешка, могут быть самыми разными.

Задача 144. Вообще, существует ровно 6 слов построенных их трех разных букв. Здесь детям предстоит достроить все 6 таких слов, напечатав в каждом слове (кроме первого) одну недостающую букву. Конечно, задача о построении всех цепочек из данных букв по сути комбинаторная, но для решения данной задачи оказывается вполне достаточно понимания того, что такое мешок бусин цепочки (или мешок букв слова).

Задача 145. Сначала попробуем найти общие бусины в цепочке и мешке. Видим, что таких бусин нет. Сделаем так, чтобы для каждой раскрашенной бусины в цепочке оказалась такая же в мешке – раскрасим в мешке две квадратные бусины (красным и синим) и одну треугольную (красным). Лучше сразу пометить в мешке и в цепочке эти три бусины галочками, чтобы больше на них не обращать внимания. Теперь сделаем так, чтобы для каждой раскрашенной бусины в мешке оказалась в цепочке такая же бусина. Рассмотрим в мешке все раскрашенные, но не помеченные бусины и сделаем  в цепочке такие же – раскрасим 4 круглые бусин (желтым, оранжевым, зеленым и голубым). Видим, что в цепочке и в мешке осталось по две нераскрашенные бусины – круглая и квадратная. Значит, каждые две бусины одинаковой формы надо раскрасить одинаковым цветом.

Задача 146. Вы, конечно, обратили внимание, что мы подобрали в этой задаче такие слова и недостающие буквы в них, чтобы у ребят получались русские слова, как бы они не вставляли недостающие буквы. Поэтому решение в этой задаче единственно.

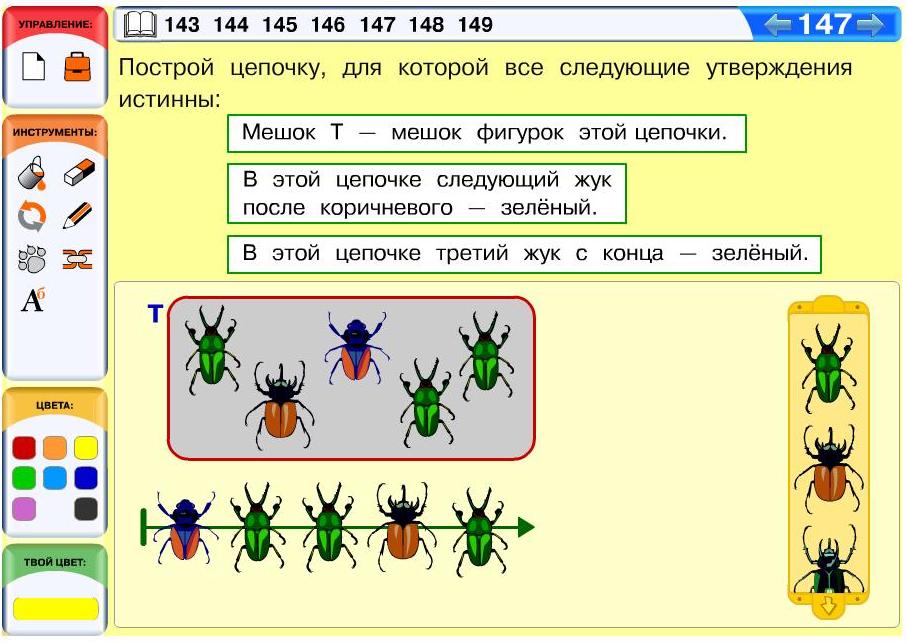
Задача 147.  В этой задаче дети впервые строят цепочку по описанию, включающему мешок фигурок этой цепочки. Однозначно определяется здесь только третья фигурка (зеленый жук). Коричневый жук может быть первым или четвертым, после него должен стоять зеленый. Остальные фигурки можно расставить как угодно. Таким образом, данная задача имеет ровно 4 решения.

Задача 148. Это первая задача на поиск слова в Словаре нового типа – в ней описание содержит мешок букв искомого слова. Сложность таких задач в том, что неизвестна первая буква слова. Это существенно увеличивает перебор, однако понятно, что первой буквой должна быть одна из букв мешка Х. В задаче известно, что искомое слово идет в Словаре позже слова ПАЛЬТО, значит первая буква нашего слова может быть буквой П, Т или Ю (на Ь слова начинаться не могут). Теперь осталось просмотреть слова на все эти буквы и попытаться найти слово, мешок букв которого – мешок Х. При этом для сравнения слов и мешка Х совсем не обязательно просматривать все буквы, вполне достаточно ориентироваться на редко встречающиеся буквы – Ю и Ь. Так, среди слов с первой П нет ни одного слова с буквой Ю, значит нашего слова среди этих слов нет.

Задача 149. Необязательная. Данную задачу, как и многие другие в нашем курсе, можно решать перебором. Поскольку монет здесь всего три вида, возможны всего 3 варианта видов монет в мешках: в одном кошельке рублевые, в другом – пятирублевые; в одном мешке двухрублевые, в другом – пятирублевые; в одном мешке рублевые, в другом – двухрублевые. Очевидно, что третий вариант не подходит, поскольку пять двухрублевых монет это всего 10 рублей, а нам нужно 16 рублей. Остальные варианты нужно проверить более внимательно.

Компьютерный урок «Мешок бусин цепочки», 2 часть

Решение задач 150 – 156 

Задача 150. Если кто-то из детей допустит в этой задаче ошибку, попросите его соединить одинаковые бусины в цепочке и в мешке в пары. В этом случае ребенок, скорее всего, найдет свою ошибку самостоятельно.

Задача 151. В этой задаче цепочки, которые получатся у разных детей, скорее всего, будут разными. Тем не менее, значение истинности первого утверждения будет у всех ребят одинаковым («истинно»). Если кого-то из детей это удивит, порассуждайте с ним, почему так получается. На самом деле, то, что есть и чего нет в данной цепочке будет полностью определяться мешком ее фигурок. В мешке фигурок этой цепочки есть две одинаковые фигурки, значит, они будут и в цепочке.

Задача 152. Если внимательно прочитать условие, становится ясно, что каждый мешок должен быть соединен ровно с одним словом. Это означает, что если бы таких слов было несколько, мы бы соединили мешок с любым из них. В данном случае для каждого из мешков в наборе есть лишь одно подходящее слово. Но слов у нас больше, чем мешков, значит, в наборе есть лишние слова, которые не будут соединены ни с одним из мешков. Поэтому в этой задаче перебор удобнее вести по мешкам. В каждом слове и в каждом мешке есть по две буквы О, поэтому ориентироваться можно только на согласные в мешках. Например, в первом мешке есть согласные П, Г и Р, ищем слово, в котором есть такие буквы. Это слово ПОРОГ, соединяем его с первым мешком и переходим ко второму мешку и т. д.

Задача 153. В силу истинности первого утверждения потребуется перебор всех слов, которые идут в Словаре раньше слова КАРАНДАШ. Таких слов довольно много, поэтому попробуем сразу сократить перебор, использовав какие-то дополнительные параметры поиска, которые вытекают из описания. Во-первых, в нашем слове 7 или больше букв (иначе второе утверждение не будет иметь смысла). Во-вторых, в искомом слове есть буквы: Ж, Ь, А. Буква Ж не является слишком часто встречающейся (например, среди слов на А, Б, В, Г, Д, нет ни одного слова с буквой Ж). Поэтому некоторые дети догадаются прежде всего просмотреть именно слова с первой буквой Ж (в них Ж точно есть). Именно среди этих слов в данном случае и оказывается данное слово.

Задача 154.Начать здесь стоит с последнего утверждения, поставив перед красной квадратной бусиной желтую круглую. Затем можно поставить синюю бусину где-то до этой пары. Теперь нужно поставить в цепочку остальные бусины практически как угодно (главное не ставить бусин между красной квадратной и желтой круглой).

Задача 155. Здесь нужно внимательное сопоставление очень похожих фигурок друг с другом. Для начала стоит определить для каждой фигурки из мешка, какой фигурке из цепочки она соответствует. Проще всего это сделать, учитывая цвет рамки и внутреннего кольца фигурок. После этого задача становится аналогичной задаче «сделай фигурки одинаковыми – раскрась нераскрашенные области».

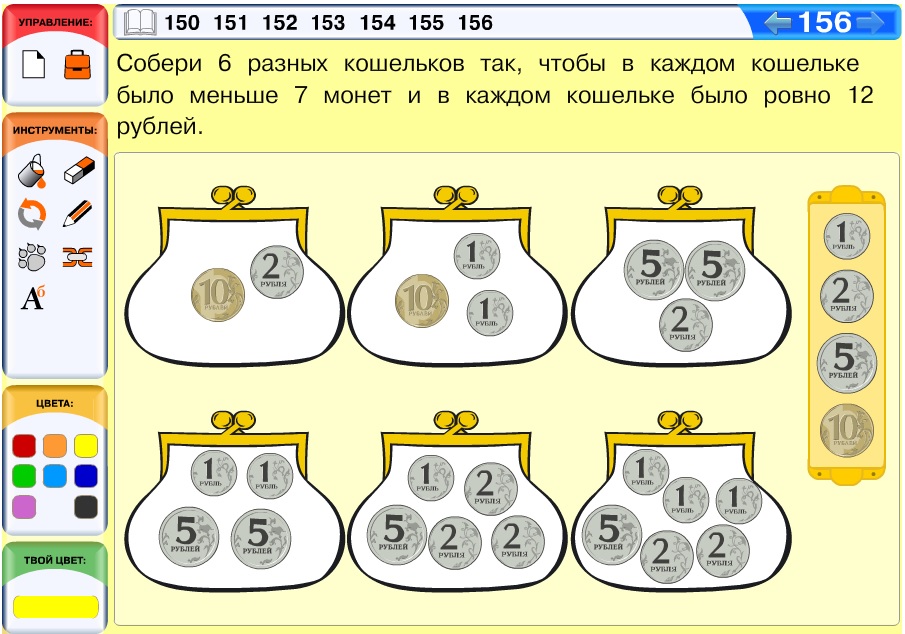
Задача 156. Необязательная. Построить по описанию шесть разных мешков методом проб и ошибок не у всех ребят получится сразу — многим потребуется выполнить перебор. Поскольку в описании имеется ограничение числа монет сверху (меньше семи), то монеты придётся «экономить». Лучше начать перебор с монеты наибольшего достоинства — монеты 10 рублей. В один мешок нельзя положить больше одной такой монеты, поэтому кладём в первый мешок одну монету 10 рублей и добавляем в мешок монеты так, чтобы в нём получилось 12 рублей. Это можно сделать двумя способами — монетой 2 рубля и двумя монетами достоинством 1 рубль. Это позволяет нам построить по описанию два мешка (в одном из них 2 монеты, в другом — 3 монеты). Теперь перейдём к монетам достоинством 5 рублей. Их можно положить в кошелёк не больше двух. Для начала положим две монеты по 5 рублей и добавим ещё монет до 12 рублей. Это тоже можно сделать двумя способами, строим ещё два мешка по описанию (в одном мешке 3 монеты, в другом — 4 монеты). Теперь положим в мешок только одну монету в 5 рублей и дополним кошелёк до 12 рублей, используя как можно больше монет по 2 рубля и как можно меньше — по 1 рублю. Получается кошелёк из одной монеты 5 рублей, трёх монет по 2 рубля и одной монеты 1 рубль (всего 5 монет). Чтобы построить ещё один кошелёк по описанию, достаточно одну из двухрублёвых монет разменять на две рублёвые.

Решение задачи урока 2  для «Водолея»

Задача 1 (Водолей).  Как и в задачах урока 1, дети находят здесь решение в ходе проб. С сильными учащимися можно по окончании решения проводить рассуждения, чтобы постепенно у ребят формировались представления о связи этих проб с арифметическими и логическими соображениями. Решения конечно при этом можно построить самые разные. Например, здесь из арифметических соображений ясно, что 5=7-2. Значит, чтобы получить 5 литров, нужно из 7 литров отлить ровно 2 литра. Это можно сделать, если предварительно получить в 3-литровой емкости 1 литр. Для этого достаточно дважды наполнить из 7-литровой емкости 3-литровую и оставшийся литр перелить в 3-литровую емкость.

Решение задачи урока 3  для «Водолея»

Задача 1 (Водолей). В этой задаче рассуждения могут быть следующими. Из арифметических соображений ясно, что 1=15 – 14. При этом 15 – это 3 раза по 5, а 14 – это 2 раза по 7. Значит, чтобы в сосуде остался 1 литр, нужно налить 3 раза по 5 литров в сосуд вместимости 7 и наполнить его подряд 2 раза.