Информатика. 2 класс Демо+методичка

Урок 20. «Вместимость. Переливание»

Первая часть листа определений посвящена знакомству с понятием «вместимость». Здесь обсуждается измерение вместимости посуды, а также единицы вместимости – литры. По содержанию данный материал больше относится к курсу математики, где его и логичнее было бы обсуждать. Однако для обсуждения второй части листа определений и решения задач необходимо, чтобы дети владели понятиями «вместимость» и «литр». При этом курсы математики, по которым учатся дети, сейчас имеются самые разные, и мы не можем быть уверены, что учащиеся с этими понятиями действительно знакомы. Таким образом, первая часть курса необходима, чтобы не нарушать принципы построения нашего курса – явное введение всех правил игры и наглядное введение основных понятий. Если ваш класс в курсе математики уже знакомился с данными понятиями, то первую часть листа определений дети могут просто быстро просмотреть.

Вторая часть данного листа определений – первое знакомство с ситуацией переливания из одного сосуда в другой (конечно, совсем простая). Именно на таких ситуациях построена известная серия задач на переливание, к решению которых мы постепенно хотим подвести детей. Если у вас есть возможность работать с компьютерными задачами о «Водолее», то дети продвинутся в этой теме существенно дальше, и вскоре на уроках математики и информатики вы сможете им предлагать классические задачи на переливание. Если класс работает только с печатными материалами, значит, придется вести работу в этом направлении более медленно и постепенно.

Главное, что необходимо понимать, работая с задачами на переливание – межпредметный характер этих задач. Это задачи в равной степени математические и информатические. К математике в таких задачах относятся в основном арифметические вычисления (не слишком сложные). С точки зрения информатики задачи на переливание – задачи на составление программы для формального исполнителя (в нашем курсе он называется Лисенок-водолей). Эту важную особенность детям бывает наиболее сложно понять. В частности, при решении задач на переливание необходимо четко представлять себе набор действий (команд), которые может выполнять объект (исполнитель). Команд существует 3 вида: а) налить полный сосуд; б) вылить все из сосуда; в) перелить воду из одного сосуда в другой. В случае переливания воды из первого сосуда во второй может получиться две ситуации: либо вода из первого сосуда помещается во второй целиком, либо вода из первого сосуда во второй целиком не помещается. Во втором случае мы наливаем ровно столько воды, чтобы заполнить второй сосуд целиком. Вода, которая не поместилась, остается в первом сосуде. Этот случай представлен на листе определений, поскольку он наиболее интересен с точки зрения получения новых объемов воды.

Решение задач из учебника

Задача 122. В этой задаче и во всех похожих на нее задачах мы готовим детей к решению более сложных задач на переливание. В таких задачах решение заключается в описании всех переливаний, что часто вызывает у детей трудности. Наиболее наглядно и полно решение таких задач выглядит в том случае, если ребенок перечисляет по порядку каждое действие и пишет, сколько жидкости получилось после этого в каждом сосуде. Поскольку это довольно необычно, к такому оформлению лучше приучать детей постепенно. Поэтому в первых задачах на переливание дети просто привыкают к переливанию по инструкции. Инструкция при этом уже составлена, а учащиеся только показывают, сколько литров воды оказывается в каждой емкости. В первой задаче для наглядности мы рисуем каждую емкость, обычно результаты переливаний отражают в таблице, позже и мы перейдем на такую форму записи.

Итак, вначале бидон и кастрюля были пустыми – в каждой емкости было 0 литров. После выполнения первого пункта инструкции в бидоне стало 3 л воды (в кастрюле осталось 0 литров). После выполнения второго пункта в бидоне стало 0 литров, а в кастрюле – 3 литра. После третьего – в бидоне стало 3 литра, а в кастрюле по-прежнему осталось 3 литра, поскольку в третьем пункте с кастрюлей никаких действий не производится. В последнем пункте кастрюлю из бидона доливаем до полной. При этом в нее нельзя налить больше 4 литров, значит, в кастрюле получается 4 литра. Оказывается, что из бидона мы вылили 1 литр, значит, там осталось 2 литра.

В этой задаче ребята должны заметить, что с помощью некоторой цепочки переливаний можно получить новое число литров. Так, в данной задаче в нашем распоряжении были только емкости в 3 литра и в 4 литра, а в конце получилось 2 литра.

Задача 123. На первый взгляд все задачи на Словарь очень похожи между собой, однако уровень их сложности будет постепенно повышаться. Как вы помните, почти во всех наших задачах на поиск слов в Словаре была известна первая буква слова. Это существенно сужает перебор и упрощает задачу. Здесь первая буква слова не известна. Это означает, что перебор придется вести среди всех слов Словаря. При этом лучше использовать сначала первое утверждение, ведь увидеть 3 буквы Е проще, чем посчитать число букв в слове. Итак, начинаем перебирать слова начиная с первого – АВАРИЯ. Первое по счету слово, в котором всего 3 буквы Е, – слово ВОСКРЕСЕНЬЕ. Но в нем больше 8 букв, поэтому продолжаем перебор дальше. В результате находим подходящее слово – ЛЕДЕНЕЦ.

Задача 124. Здесь дети повторяют операцию сложения мешков. Способы решения подобных задач могут быть разными. Некоторые дети перебирают мешки попарно, пересчитывая, сколько бусин в парах, пока не встретят нужные числа. Чаще дети сразу пересчитывают бусины во всех мешках (удобней подписать полученные числа над мешками) и складывают попарно уже числа. Бывают и такие учащиеся, которые пытаются дополнить один из мешков до нужного числа бусин.

Задача 125.  В целом данная задача аналогична задаче 122. Оформление выполнения инструкции, которое здесь предлагается, не столь наглядное, как в задаче 122, но стандартное и более краткое. Именно такую таблицу удобно строить, решая более сложные задачи на переливание. В классических задачах на переливание обычно требуется описать (составить инструкцию), как с помощью некоторых переливаний, имея сосуды определенной вместимости, получить требуемое число литров. Пока в курсе дети только выполняют инструкции – привыкают к способу записи, готовятся к решению таких задач. Как и в задаче 122, ребята могут здесь проследить, как в процессе переливаний получаются новые количества литров, то есть такие, которые не равны вместимости сосудов. Так, в данном случае, имея только сосуды в 3 л и 5 л, дети смогли получить 2 л и 4 л воды.

Задача 126. Вообще поиск двух одинаковых мешков в некоторой совокупности – дело не такое уж и легкое. Если мешков и фигур в мешках много, то без определенной системы не обойтись. В данной задаче некоторые учащиеся, возможно, случайно наткнутся на решение, но мы советуем вам уже сейчас обращать внимание на приемы поиска одинаковых мешков на будущее. Для этого после окончания решения необходимо выслушать все идеи ребят, которые облегчили им работу над задачей. Конечно, можно использовать полный перебор по определенной системе, сравнивая все мешки между собой, но это очень долго. Более удобно делить мешки на группы по определенному признаку и дальше сравнивать мешки в группах уже только между собой (это существенно уменьшит число сравнений). Признаки ребята могут выделить самые разные, например число фигурок в мешке. Во всех мешках по 3 фигурки, а в одном – 4, значит, его можно сразу отбросить (зачеркнуть), для него такой же уже не найдется. Далее оставшиеся мешки можно делить по наличию в них красного лимона: в трех мешках его нет, в остальных есть. Первые 3 мешка легко сравнить между собой и выяснить, что среди них нет двух одинаковых, вычеркиваем их тоже. Оставшиеся мешки можно делить, например, по наличию в них желтого яблока, получится две группы по 4 мешка. В каждой группе мешки сравниваем между собой и находим одинаковые: второй во втором ряду и последний в третьем.

Задача 127. Необязательная.  К настоящему моменту дети уже должны понимать, что разные бусины должны отличаться либо по цвету, либо по форме. Если все бусины в мешке должны быть треугольными, то все они должны быть разных цветов.

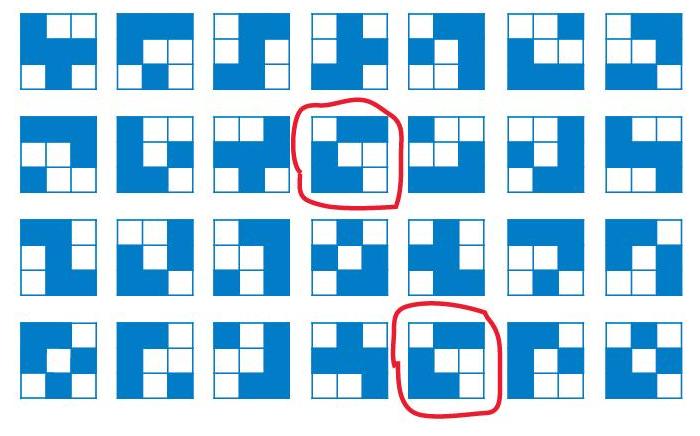
Задача 128. Необязательная. Возможно, кому-то из ребят повезет, и он найдет решение простым проглядыванием. Однако, большинству детей это не удастся – слишком много здесь фигурок и слишком они похожи между собой. Полный перебор и сравнение каждой фигурки с каждой делать здесь оказывается слишком долго. Оптимальный вариант – деление фигурок на группы по некоторому признаку. Признаки могут быть при этом разные. Например, нетрудно заметить, что в каждой фигурке по 5 закрашенных клеток. При этом в некоторых фигурках эти клетки расположены все вместе (связаны между собой), в других расположены 4 вместе и 1 отдельно, в третьих – три вместе и две отдельно (тоже вместе или поодиночке). Так получаем три или четыре группы, внутри которых уже гораздо легче сравнить фигурки друг с другом.

Задача 129. Необязательная. В данной задаче мы ведём пропедевтику темы «Разбиение мешка на части». Действительно, по сути, в этой задаче выполняется действие, обратное сложению мешков: по мешку-сумме строятся исходные мешки. Такое действие и является разбиением мешка. Конечно, исходные мешки определяются по результату сложения не однозначно, вариантов таких пар существует много. Если мы хотим сузить область решения, то необходимо накладывать на мешки дополнительные условия. Так, в данном случае в мешке К и в мешке У должно быть одинаковое количество букв, и в каждом из них все буквы должны быть разными. В мешке Т 12 букв, значит в каждом из исходных мешков было по 6 букв. Распределяя буквы в мешки так, чтобы в одном мешке не было одинаковых букв, получаем два одинаковых мешка, состоящих из букв А, Ч, Ф, С, Ю, Я.

Лист определений «Знакомимся с Водолеем»

На этом уроке дети знакомятся с новым компьютерным модулем «Водолей». Дизайн задач про Водолея несколько отличается от других компьютерных задач (и опирается на другие программные возможности), поэтому в каждом уроке эти задачи находятся в отдельной вкладке (и имеют собственную нумерацию). Компьютерный модуль «Водолей» имеет в курсе большое значение. С точки зрения информатики, ребята знакомятся с первым исполнителем. При этом в ходе решения компьютерных задач ребята интуитивно усваивают понятие «команда», «программа», «результат выполнения программы», «условия», «ограничения» и проч. Все это пригодится детям, когда в курсе 3 класса эти понятия будут вводиться на листах определений и использоваться в задачах. На данном этапе дети накапливают опыт для такого обсуждения. С точки зрения математики дети в ходе работы с компьютерным ресурсом учатся решать классические задачи на переливание: улавливают основные закономерности, знакомятся с правилами записи и проч.  В данном случае компьютерный ресурс оказывается существенным методическим подспорьем. Во-первых, он отражает текущее состояние всех сосудов на экране. Во-вторых, он записывает все сделанные ребенком переливания в программу. Наконец, он отслеживает момент, когда в одном из сосудов получилось столько литров, сколько нужно было получить в задаче. Таким образом, компьютерная программа «Водолей» полностью снимает с ребенка всю нагрузку по фиксации переливаний и оформлению решения. Учащийся при этом может полностью сосредоточиться на пробах и экспериментах. В случае, если эти пробы увенчались успехом – ребенок получил нужное число литров (возможно, случайно), он может вернуться и просмотреть в программе, какие его действия к этому привели. Таким образом, работа в программе «Водолей» позволяет детям накопить необходимый опыт для последующего самостоятельного решения задач на переливание в курсе математики.

При знакомстве с компьютерным ресурсом «Водолей» можно попросить ребят открыть первую задачу про Водолея и немного освоиться с дизайном таких задач: попробовать выполнить разные команды, посмотреть, как результат их выполнения будет отражаться на экране и проч. Затем в индивидуальном порядке можно ответить на все возникшие вопросы.

На экране с задачами о «Водолее», как и в задачах компьютерных уроков можно выделить рабочую область и ящик инструментов. В рабочей области сверху, как обычно располагается линейка перемещения по задачам, ниже – условие задачи (в выделенном прямоугольнике), еще ниже – основное рабочее пространство. Условия всех задач о Водолее однотипные – с помощью данных сосудов получить некоторое число литров воды, поэтому сформулированы они максимально кратко и основная информация в этом условии – число (литров, которые нужно получить). Под условием расположено собственно поле решения задачи, на котором отображаются результаты выполнения всех команд, которые дает учащийся. В ящике инструментов (в левой полосе) находится собственно пульт управления, то есть набор всех кнопок, которые соответствуют командам Водолея, окно программы, в котором словами отображаются все данные команды и управляющие кнопки «начать сначала», «сохранить и выйти».

Водолей может выполнять 3 вида команд:

Первый вид команд – заполнить (из-под крана) некоторый сосуд (А, Б или В) целиком. Кнопки команд этого вида расположены в первом ряду кнопок. Результат выполнения этих команд не зависит от исходного состояния сосуда и всегда одинаков – полный сосуд. Если сосуд был пуст он наливается целиком, если сосуд был частично заполненный, то доливается до полного. Если эта команда дается в случае полного сосуда, с ним не происходит ничего.

Второй вид команд – вылить (в раковину) всю воду из некоторого сосуда (А, Б или В). Кнопки команд этого вида расположены во втором ряду кнопок. Результат выполнения этих команд не зависит от исходного состояния сосуда и всегда одинаков – пустой сосуд. Если в сосуде была вода, она вся выливается, если сосуд и был пуст, с ним не происходит ничего.

Третий вид команд – перелить из одного сосуда в другой столько воды, сколько в него поместится (остальная вода остается в первом сосуде). Кнопки команд этого вида расположены в третьем и четвертом ряду кнопок. Результат выполнения этих команд (состояния первого и второго сосуда) зависит от исходного состояния сосудов. Как первый, так и второй сосуды могут оказаться в результате выполнения этих команд: полными, пустыми, частично заполненными. В частности, если первый сосуд пуст или второй – полон, с сосудами не произойдет ничего (в первом случае переливать нечего, во втором – некуда).

Решение задач 1 – 4  для «Водолея»

Задача 1 (Водолей). Начинается серия, конечно, с самых простых задач, таких, где программа для Водолея не будет длинной, и ребята смогут полностью проследить выполнение всех ее команд. Почти все дети здесь сразу догадаются, что 8=5+3, поэтому для решения задачи нужно, сначала по очереди наполнить емкости вместимостью 5 и 3 литра, а затем вылить воду из них в 10-литровую емкость. После этого в ней станет 8 литров, стрелочка около этой емкости станет оранжевой. Это означает, что задание выполнено.

Задача 2 (Водолей). Решение этой задачи уже не настолько очевидно, как решение предыдущей, далеко не все дети смогут решить ее с ходу. Таким детям надо посоветовать искать решение в ходе подбора, пробуя разные варианты переливания. Лучше по ходу записывать все новые количества литров, которые ребенок смог получить. Ясно, что сливая емкости 3 л и 5 л можно получить 8 л. Что можно получить, если переливать из одного сосуда в другой? Если переливать из 5-литрового в 3-литровый, можно получить 2 литра. 4 л можно представить как сумму 2 л и 2 л, значит, чтобы получить нужные нам 4 литра, достаточно повторить процедуру переливания из 5-литрового сосуда в 3-литровый дважды.

Задачи 3 и 4 (Водолей). В ходе решения данных задач полезно использовать опыт решения предыдущих, ведь два из трех сосудов имеют тот же объем (5 л и 3 л). Мы уже знаем, как получить 4 л и это можно использовать в решении. В частности, если из сосуда с четырьмя литрами наполнить 3-литровый сосуд, то останется ровно 1 литр. А если к 4 л добавить всю воду из полного 3-литрового сосуда, то получится ровно 7 литров. Конечно, это лишь один из вариантов решения, у ребят могут быть другие решения, в том числе очень длинные. Если вы видите, что у сильного учащегося программа чрезмерно длинная и содержит «пустые» куски, то есть такие фрагменты программы, которые не влияют на решение, можно попросить его начать сначала и построить программу покороче.

Решение компьютерных задач 139 – 142 

Задача 139. Эту задачу можно решать как с помощью арифметических соображений, используя состав числа 12, так и информатическими методами (перебора или проб и ошибок). Перебор мы всегда советуем начинать с монет наибольшего достоинства. Положим в один из мешков монету в 10 рублей (больше таких монет положить нельзя) и попробуем положить в мешок еще 2 монеты так, чтобы в мешке стало 12 рублей. В ходе проб выясняем, что в мешок нужно положить 2 монеты по рублю и других вариантов быть не может. При построении второго мешка мы уже не можем использовать монету в 10 рублей (иначе мешок станет таким же, как первый). Начинаем пробы с монетами в 5 рублей. В ходе этих проб выясняем, что их можно положить не больше двух. Для начала положим две таких монеты и попробуем дополнить мешок еще одной монетой, чтобы в мешке стало 12 рублей.

Задача 140. Чтобы не запутаться, лучше искать и класть в мешок названия дней недели в определенном порядке, например, в календарном порядке соответствующих дней или в алфавитном порядке первых букв слов. Во втором случае дети сначала ищут слова на букву В – ВТОРНИК и ВОСКРЕСЕНЬЕ, затем слова на букву П – ПОНЕДЕЛЬНИК и ПЯТНИЦА, потом слова на С – СРЕДА и СУББОТА и наконец, слово ЧЕТВЕРГ.

Задача 141. В этой задаче из истинности первого утверждения в частности следует, что в нашей цепочке ровно одна красная фигурка и ровно одна желтая фигурка (во всех других случаях утверждение не будет иметь смысла). Из истинности второго и третьего утверждения следует, что в цепочке ровно одно яблоко, ровно одна слива и есть груша. При этом в цепочке должно быть хотя бы 3 фигурки, а значит, в цепочке должна быть хотя бы одна зеленая фигурка. Таким образом, цепочка может состоять из 3 фигурок (груши, яблока и сливы трех разных цветов), а может быть и длиннее за счет груш зеленого цвета.

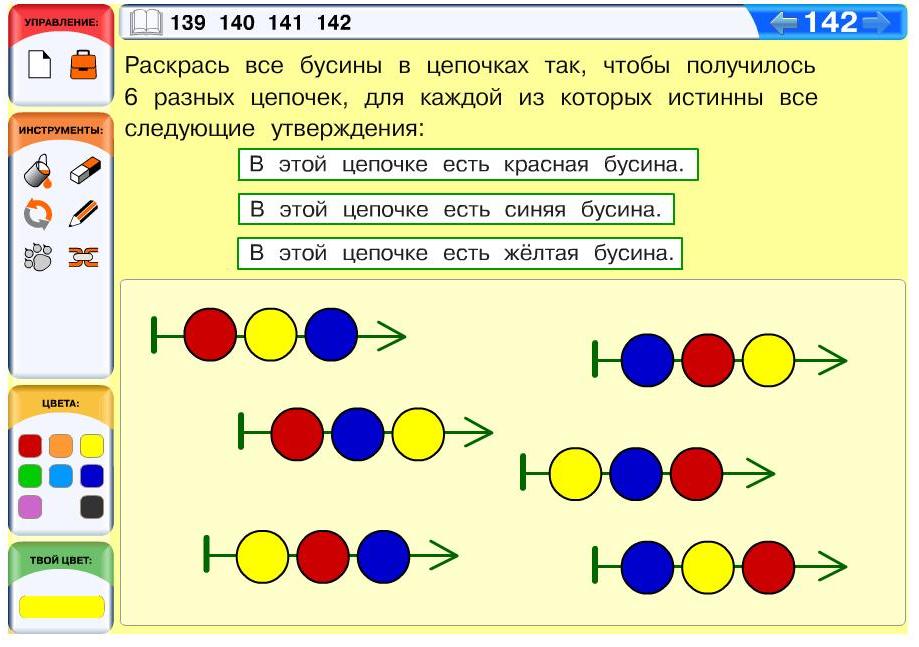
Задача 142. Необязательная. По содержанию это комбинаторная задача. Такие задачи дети могут решать методом проб и ошибок, перебором, используя рассуждения. Из истинности данных утверждений следует, что в каждой из цепочек должна быть ровно одна красная, ровно одна синяя и ровно одна желтая бусина. Раскрасим первую цепочку произвольно, например, первую бусину раскрасим красным, вторую – синим, третью – желтым. Теперь раскрасим вторую цепочку так, чтобы она отличалась от первой. Для этого достаточно поменять цвет хотя бы одной бусины. Например, поменяем цвет второй бусины – раскрасим ее желтым, а третью бусину – синим. После этого можно поменять цвет первой бусины и т. д.