Информатика. 2 класс Демо+методичка

Урок 17. «Выравнивание, решение необязательных задач», 1 полугодие

Как и в курсе 1 класса, мы советуем вам в этом году после каждой контрольной работы проводить уроки выравнивания. Цель уроков выравнивания – продвинуть всех учащихся класса в изучении материала курса ровно настолько, насколько позволяет уровень каждого конкретного ученика. Это урок, на котором слабые ученики смогут ликвидировать свои пробелы в знаниях, а сильные – попробовать свои силы в решении задач повышенной сложности. На этом уроке вы сможете реализовать индивидуальный подход к каждому ребенку, предложив ему собственный набор задач из числа тех, которые мы заготовили к этому уроку (как из учебника, так и из компьютерной составляющей).

Разделение задач на обязательные и необязательные в данном уроке условно и не регламентирует работу настолько жестко, как на уроках изучения материла. В основном, как обязательные в этом уроке помечены задачи, которые можно предлагать всем учащимся, в том числе и самым слабым. Необязательные задачи нужно предлагать выборочно, в зависимости от уровня конкретного учащегося.

Решение задач из учебника

Задача 100. Необязательная. Здесь дети повторяют тему «Одинаковые цепочки» и лексику, связанную с порядком бусин в цепочке. Конечно, эту задачу можно решать методом проб и ошибок. Но рациональная стратегия – сразу принять во внимание, что нужно будет построить две одинаковые цепочки, поэтому цепочки как минимум должны состоять из одного и того же набора букв. Есть смысл сразу разделить все буквы на две кучки – для одной и другой цепочки. Можно провести карандашную черту между этими двумя группами. Дальше есть смысл из букв одной группы построить первую цепочку, используя данные утверждения. Как обычно в таких задачах очень важно, в каком порядке использовать условия. Общий принцип прост – использовать сначала утверждения, которые устанавливают положение букв однозначно. Например, среди данного набора букв (М, К, О, А, Н, А, Т) только две одинаковые, они и будут первой и пятой буквами данного слова. Теперь понятно, что оставшаяся гласная буква (О) будет стоять на втором месте. После этого остается лишь одна пара пустых мест стоящих подряд, там должны стоять буквы Н и М. Теперь используем последнее утверждение и получаем слово КОМНАТА. Остается построить из оставшихся во второй группе букв такую же цепочку букв.

Задача 101. Необязательная. Для кого-то эта задача может оказаться сложной, поскольку в картинке имеется много мелких областей, которые сложно заметить, и большая область, которую трудно охватить взглядом. Зрачок глаза (черный кружок) по нашим договоренностям областью считать не надо. Всего в картинке оказывается 7 областей: 2 области гривы, 2 области глаза, 1 область тела и 2 области ног.

Задача 102. Понаблюдайте, есть ли в вашем классе ребята, которые пытаются определять истинность первого и второго утверждения без опоры на Словарь. В первом утверждении это наверняка могут сделать почти все ваши дети. Первые буквы слов в Словаре идут в алфавитном порядке, буква И в алфавите идет раньше Й, поэтому и слово ИГРУШКА идет раньше слова ЙОД. Со вторым утверждением ситуация сложнее, оба слова начинаются на букву М и даже имеют одинаковые вторые буквы. Здесь можно просто предложить детям выдвинуть какое-то обоснованное предположение, а потом проверить его по Словарю. Если в процессе этого разговора ребенок смог объяснить, почему слово МАРТ идет в Словаре позже слова МАЙ, ему несложно будет объяснить, почему третье утверждение ложно. Слово НИКОГДА должно идти в Словаре раньше слова НОЛЬ, поэтому не может быть следующим за ним.

Задача 103. Необязательная. Здесь ребята снова работают с цепочкой месяцев года, но здесь порядок месяцев по содержанию задачи не важен, поэтому для нас она выступает лишь как цепочка соответствующих названий. Конечно, не во всех названиях месяцев есть и буква А и буква Р, остальные слова дети должны пометить галочкой. Таких слов оказывается ровно 7.

Задача 104. Необязательная. Здесь, чтобы утверждение имело смысл, в каждой из цепочек должен быть ровно один желтый лимон и ровно одна синяя луковица. Поскольку в каждой из наших цепочек лимон вообще один, значит его сразу можно раскрасить в желтый цвет. Лимон должен идти раньше синей луковицы, поэтому третью фигурку в каждой цепочке нужно раскрасить синим. Значит, цепочки можно сделать разными только за счет первой фигурки в цепочке – первые луковицы нужно раскрасить в разные цвета. При этом синий цвет использовать нельзя, значит в одной из цепочек первую луковицу нужно оставить нераскрашенной. Если вы опасаетесь, что дети не догадаются до такого решения, предложите им перед началом решения просто вычеркнуть одну из цепочек и решать задачу для 7 цепочек.

Задача 105. Учащемуся, который затрудняется с решением этой задачи нужно предложить вести перебор букв с опорой на алфавитную линейку.

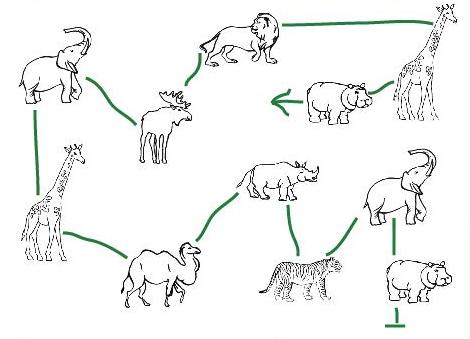
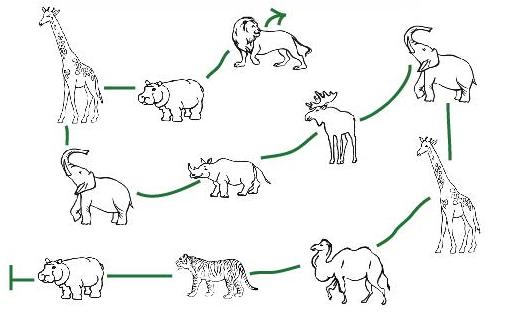
Задача 106. Попытаемся проанализировать свои действия в ходе решения этой задачи. Во-первых, мы читаем все утверждения и обдумываем каждое из них по отдельности, имея в виду, что при построении цепочки нам придется заботиться обо всех одновременно. Во-вторых, мы прикидываем, как будем добиваться выполнения каждого из требований. Вот пример возможного рассуждения: «Поставить на какое-то заданное место слона или жирафа – дело нехитрое; чтобы фигурки на первом и последнем местах были одинаковые, надо иметь запас из двух одинаковых фигурок. Ага, есть два бегемота, а также два жирафа и два слона. Но мы не можем поставить на первое и последнее места ни жирафов, ни слонов, иначе потом не сможем обеспечить истинность второго и третьего утверждений». Поняв, что у нас много свободы в выборе, мы начинаем и заканчиваем цепочку бегемотами – поставим около бегемотов знаки начала и конца цепочки. Дальше проще цепочку строить с конца. Соединяем последнего бегемота с жирафом, потом вставляем еще две какие-нибудь фигурки, но не больше одного слона, затем идет слон (пятый с конца), далее последовательно все оставшиеся фигурки (ведь все фигурки должны войти в цепочку!) и, наконец, первый бегемот. Обратите внимание, что нам пришлось производить несложные арифметические действия и много простых умозаключений.

Можно обсудить с детьми их подходы и способы рассуждения при решении этой задачи, а тех, кто быстро справился с заданием, попросить записать, как они рассуждали и в каком порядке действовали. Посоветуйте детям сначала решать задачу с карандашом и резинкой, чтобы было легко исправлять ошибки. Решать задачу будет легче, если вырезать фигурки и сложить нужную цепочку на столе. Если у вас есть возможность, заготовьте несколько копий этой страницы для вырезания. Впрочем, можно обойтись и просто небольшими квадратиками бумаги, на которых написаны названия животных. Предложите такой облегченный способ детям, которые затрудняются в решении.

Задача 107. Необязательная. Данная задача может показаться учащимся неожиданной. Действительно, в нашем курсе дети обычно определяют истинность утверждений для цепочек (или других объектов) представленных явно, чаще всего просто нарисованных, то есть объектов полностью определенных. Здесь же идет речь о некоторой цепочке, о которой известно лишь то, что она состоит из пяти бусин. На самом деле, чтобы определить истинность данных утверждений, ничего больше знать о цепочке и не нужно. Однако, такая ситуация может поставить ребенка в тупик. Если так и случилось, посоветуйте ученику нарисовать любую цепочку из 5 бусин и определить истинность утверждений для нее. После того как задача будет решена, стоит вернуться к условию и спросить ребенка, какими будут значения истинности для другой цепочки из пяти бусин. Поскольку все данные утверждения относятся только к порядковым номерам бусин в цепочке (а не к свойствам этих бусин), то значения истинности для всех цепочек из 5 бусин будут одинаковыми – первое и последнее утверждения истинны, второе и третье – ложны.

Задача 108 предназначена в основном для сильных учащихся. Самым сложным в этой задаче является то, что нужно добиться ложности того или иного утверждения. Еще одна трудность в том, что возможностей для построения цепочки слишком много. Обратите внимание, не пытался ли кто-нибудь из детей произвести арифметические подсчеты: например, узнать, какой номер от начала будет у пятой фигурки с конца.

Задача 109. Необязательная. При решении задачи можно пойти разными путями. Первый – проверить для каждой мышки все три утверждения и остановиться, как только все они станут ложными. Второй – брать поочередно утверждения, проверять их для всех мышек и по ходу отбрасывать мышек, для которых утверждения истинны. Третий – сформулировать истинные утверждения, которые имеют то же содержание, что и данные ложные (построить отрицание). В данном случае получим утверждения:

На этой мышке не красная юбка.У этой мышки не красный бантик.Юбка и майка на этой мышке разных цветов.

Задача 110. Необязательная. В случае затруднений подобные задачи можно посоветовать решать на полоске бумаги, оставляя пробелы между цифрами после каждого использованного утверждения, чтобы следующую цифру можно было поставить на любое место.

Например, читаем первое утверждение, получаем такую последовательность:

…3…9.

Читаем второе утверждение, видим, что оно не связано с первым, можно пока его пропустить и использовать третье. Получаем две возможности:

…3…6…9… или …6…3…9…

Читаем четвертое утверждение, получаем три возможности:

5…3…6…9…,  3…5…6…9  или  5…6…3…9.

Теперь, используя последнее утверждение, из получившихся вариантов выбираем те, где цифра 3 идет раньше цифры 5. Получаем:

3…5…6…9.

Затем вернемся ко второму утверждению и вставим цифру 2. Получаем две возможные цепочки:

35629 или 35692.

Для облегчения работы над задачей можно применять два приема: разумный выбор порядка использования утверждений (ведь мы работаем по описанию) и группировку по смыслу утверждений, которые относятся к одним цифрам. Так, если прочитать и проанализировать сразу все утверждения, то проще всего сначала использовать третье и четвертое и получить последовательность:

5…6…9.

Теперь добавляем сюда последнее утверждение и получаем:

3…5…6…9.

Осталось использовать второе утверждение, и мы получим ответ.

Обратите внимание на тех ребят, которые, получив неправильный ответ, настаивают на нем. Очевидно, эти учащиеся не выполнили последнее задание или выполнили его формально. Выработку умения грамотно выполнять проверку мы считаем одной из основных задач курса. Именно для этого мы иногда помещаем подобные указания, их ни в коем случае нельзя пропускать (даже в том случае, если учащийся получил правильный ответ).

Задача 111. Напомним, что при поиске двух одинаковых мешков в наборе дети могут использовать разные стратегии. Первая стратегия – хаотичное просматривание (метод проб и ошибок), которое в ряде случаев позволяет найти решение. Вторая – полный перебор и сравнение каждого мешка с каждым. В отличие от первой она позволяет найти решение наверняка, но занимает довольно много времени. Поэтому проще использовать третью стратегию – деление мешков на группы по некоторому признаку и сравнение мешков только внутри своей группы. Признаки при этом могут быть разными. В данной задаче можно, например, использовать число фигурок в мешках. Мы видим, что в трех мешках по 8 фигурок и в трех мешках по 7 фигурок. Ясно, что в группе из трех мешков найти два одинаковых оказывается не так уж сложно.

Компьютерный урок  «Выравнивание. Решение задач. 1 полугодие»

Решение задач 122 – 129

Задача 122. Конечно, в нашей цепочке обязательно должны быть 4 фигурки: волк, бобр, белка и заяц, поскольку в противном случае одно из первых двух утверждений не будет иметь смысла. Наибольшее число фигурок в цепочке ограничивается библиотекой фигурок, ведь все фигурки должны быть разными. Что касается порядка фигурок, то два утверждения о порядке (первое и второе) не связаны между собой, поэтому использовать их можно по отдельности.

Задача 123. Как и во многих других задачах, здесь поможет деление задачи на подзадачи. Так среди бусин не будет двух одинаковых, в том случае если не будет одинаковых среди бусин: треугольной, квадратной и круглой форм. Точно также можно делить бусины не по формам, а по цветам. Например, среди данных бусин есть три синих бусины – круглая, квадратная и треугольная. Разных синих бусин может быть не больше трех, значит, синим цветом в этой задаче мы пользоваться уже не можем. Также здесь есть две оранжевые бусины – квадратная и круглая, значит можно раскрасить в оранжевый цвет одну треугольную и больше оранжевым здесь пользоваться нельзя. Аналогично, рассматриваем желтые, затем голубые бусины. После этого перебираем по очереди все оставшиеся цвета, пока все бусины не оказываются раскрашенными.

Задача 124. Утверждения в данной задаче независимы друг от друга, поэтому их можно использовать по отдельности. Тем не менее, используя следующее утверждение, дети не должны нарушать истинность предыдущего. Можно заранее принять к этому какие-то меры или каждый раз начинать проверку утверждений с начала. В качестве необходимых мер можно стараться каждый раз двигать только две фигурки, о которых идет речь в утверждении, а все остальные оставлять не месте. Например, читая первое утверждение, понимаем, что вторую и третью фигурки можно просто поменять местами. Затем в силу второго утверждения меняем местами четвертую и пятую фигурки, а в силу последнего утверждения – первую и последнюю.

Задача 125. Одна из стратегий решения этой задачи состоит в том, чтобы называть (вслух или про себя) буквы русской алфавитной цепочки и искать такие же буквы в мешке. Если некоторая буква алфавита найдена в мешке, нужно пометить ее (например, галочкой). Если буква не найдена – напечатать ее в одном из окон. Такая стратегия поможет детям постепенно уменьшать число просматриваемых букв и по ходу находить свои ошибки.

Если вы будете предлагать эту задачу слабым учащимся, можно предоставить им возможность воспользоваться алфавитной линейкой. Конечно, у слабых детей столь объемная задача займет существенно больше времени.

Задача 126. Подходящих цепочек здесь много. Один из вариантов – цепочка из восьми круглых бусин разных цветов (выстроенных в любом порядке). Цепочка может быть и гораздо длинней, но не длиннее 16 бусин, поскольку у нас 8 разных круглых и 8 разных треугольных бусин (квадратные бусины нам использовать нельзя). Кроме того длина цепочки ограничена и возможностями компьютерного инструмента «цепочка» (мы может построить только такую цепочку, которая умещается на одной строке).

Задача 127. Это сложная задача, которая требует для решения перебора всех слов Словаря, поскольку первая буква искомых слов неизвестна. Чтобы не запутаться, проще всего перебирать слова Словаря с начала. Можно при этом пользоваться прокруткой или поиском слов по первой букве. Видим, что в Словаре нет слов заканчивающихся на «ИЙ» с первыми буквами от А до П. Первое по порядку слово, заканчивающееся на «ИЙ» – слово РУССКИЙ, но в нем не 5 букв, как требуется, поэтому оно нам не подходит. Аналогично не подходит следующее слово, заканчивающееся на «ИЙ» – слово ТРЕТИЙ. Так мы продолжаем перебор, пока не находим слово УЗКИЙ. Оно нам подходит, заполняем окна в первом слове и продолжаем перебор дальше.

Задача 128. Первая часть задачи заключается в том, чтобы выбрать из этих четырех две цепочки, состоящие из одного и того же набора бусин. Это можно сделать по-разному, в том числе методом исключения. Так видим, в первой цепочке есть треугольная фиолетовая бусина, которой нет ни в одной другой цепочке, значит, первая цепочка нам не подходит. В третьей цепочке есть фиолетовая квадратная бусина, которой нет ни в одной другой цепочке, значит, она нам тоже не подходит. Остаются вторая и четвертая цепочки, из них и можно построить две одинаковые цепочки, переставляя бусины.

Задача 129.Эту задачу можно решать методом проб и ошибок, а можно организовать перебор и рассмотреть все возможные случаи. Итак, если в мешке есть пятирублевая монета, то нужная сумма уже набралась (и получился один из нужных нам мешков). Теперь становится понятно, что в других мешках такой монеты уже не будет (как и монеты в 10 рублей) – там будут только монеты по 2 рубля и по 1 рублю. При этом монет по 2 рубля может быть не больше двух, то есть два, одна или ноль. В каждом из этих случаев у нас достраивается один из мешков по описанию. Всего получается 4 мешка.