Информатика. 2 класс Демо+методичка

Урок 12. «Раньше – позже. Если бусины нет. Если бусина не одна»

Ребята уже знакомы с ситуациями, когда утверждения не имеют смысла смысла. Проблема бессмысленности может встать и в утверждениях с понятиями раньше/позже. Так, утверждение «В этой цепочке пеликан идет раньше гуся» мы понимаем следующим образом: «В этой цепочке встречается только один пеликан и только один гусь, при этом пеликан идет раньше гуся». Данное утверждение не имеет смысла, если пеликан или гусь, либо встречается в цепочке не по одному разу, либо вообще не встречается. Это утверждение ложно, если в цепочке есть только один пеликан и только один гусь и они идут в другом порядке (пеликан позже гуся).

Все задачи, относящиеся к листам определений «Раньше – позже. Если бусина не одна», «Раньше – позже. Если бусины нет» помечены как необязательные, как, впрочем, и сами листы определений. Постараемся объяснить, как работать с этими листами. Придерживаясь идеи полноты и естественности курса, мы честно пытаемся здесь предупредить ребят относительно ситуаций, с которыми они могут столкнуться, однако понимаем, что для детей материал этот достаточно сложен. Поэтому на данном этапе нет смысла требовать его усвоения от всех учащихся. Материал этих листов определений не включен нами и в следующую контрольную работу.

Тем не менее, мы считаем, что сильным ученикам нужно предоставить возможность изучить данный материал в полном объеме (прочитать листы определений и решить задачи), а средним хотя бы познакомиться с ним. В дальнейшем мы будем избегать задач на сортировку утверждений с понятиями «раньше/позже» на имеющие смысл и не имеющие смысла. Для нас важно, чтобы при решении задачи «Построй цепочку, в которой буква С идет раньше буквы К» ребенок вместе с нами понимал, что буква С и буква К в этой цепочке должны существовать и причем в единственном варианте.

В перспективе мы хотим добиться понимания этого материала от всех учащихся. Как выполнить эту долгосрочную задачу, решать вам. Можно постепенно расширять круг ребят, решающих задачи с подобными ситуациями, возвращаясь с ребятами к этим листам определений. Можно познакомить с этим материалом сразу большинство ребят (за исключением самых слабых). При таком варианте вы сможете отметить для себя детей, которым так и не удалось разобраться в этом сложном материале. Позднее при решении подобных задач на них следует обратить особое внимание. После того как основная масса детей усвоит материал, можно поработать индивидуально с самыми слабыми учащимися. Возможно, вы изобретете какой-то другой, свой способ работы над этим материалом. Главное здесь – постепенность, накопление у учащихся опыта, так как такой материал сложно «взять приступом».

Решение задач из учебника

Задача 74. Необязательная. Здесь первое утверждение не имеет смысла, поскольку в цепочке нет лимона, второе утверждение не имеет смысла, поскольку в цепочке нет ананаса, а последнее – так как в цепочке нет банана.

Задача 75. Необязательная. Здесь не имеет смысла первое утверждение, поскольку красных квадратных бусин здесь две. Кроме того, не имеет смысла последнее утверждение, поскольку красных бусин в цепочке три. В отличие от предыдущей задачи, здесь дети могут допустить ошибки. Так многие учащиеся при анализе первого утверждения рассуждают следующим образом «Синяя бусина в цепочке идет последней. Она позже любой из красных квадратных бусин. Значит утверждение истинно». На самом деле данная ситуация не снимает некорректности в формулировке утверждения – в утверждении не понятно, о какой бусине идет речь.

Задача 76. Эта задача интересна тем, что включает в себя почти всю лексику, относящуюся к порядку элементов в цепочке. Важно, чтобы дети не запутались в терминах и связали разные понятия между собой. В результате выполнения инструкции получается слово ЗИМОРОДОК.

Задача 77. Детям, которым трудно принимать во внимание одновременно три утверждения, посоветуйте строить цепочку методом проб и ошибок. Можно при этом принять во внимание хотя бы одно утверждение, чтобы потом было меньше работы. Исходя из первого утверждения, можно поставить лимон с долькой первым, лимон с веточкой – вторым, а остальные поставить в цепочку произвольно. Теперь читаем второе утверждение. Если оно истинно, то переходим к следующему утверждению, а если – ложно, меняем апельсины в цепочке местами. Конечно, в ходе проб детям лучше работать карандашом.

Задача 78. Необязательная. В этой задаче сразу бросается в глаза, что желтый квадратик есть во всех фигурках, кроме одной – значит, ее не рассматриваем. Голубой цвет из оставшихся фигурок есть только в трех. Осталось выбрать из этих фигур такую, в которой нет фиолетового квадратика.

Задача 79. Обратите внимание детей на то, что найти значения утверждений требуется именно для данной цепочки месяцев, соответствующей одному отдельно взятому году. Заметьте, что, вообще говоря, можно построить такую цепочку месяцев (и даже идущих подряд в реальной хронологии), в которой январь идет позже февраля. Было бы хорошо, если бы дети привели пример такой цепочки. Здесь первые три утверждения истинны, остальные два ложны.

Задача 80. Если вы видите, что кто-то из ребят затрудняется с решением этой задачи, посоветуйте ему сначала собрать на столе все бусины, о которых идет речь в условии задачи (круглая красная, треугольная желтая, синяя квадратная, оранжевая любой формы). Конечно, в цепочке могут быть и другие бусины, но это не обязательно. Затем можно строить цепочку методом проб и ошибок, передвигая бусины на столе и проверяя истинность утверждений.

Задача 81. В этой задаче мы предлагаем ребятам подумать о взаимосвязи двух одномерных таблиц для одного мешка. Конечно, общее число бусин в обеих таблицах должно быть одним и тем же. Также должно быть одним и тем же число бусин одинаковой формы. Именно на этой идее и основано решение данной задачи.

Задача 82. Необязательная. Спросите нескольких детей, кто у них второй в очереди. Окажутся, скорее всего, дети с разными именами. В этой простейшей ситуации находят отражение два важных обстоятельства. Первое – произвольность имени: ты можешь назвать детей как хочешь. Ситуация здесь как бы обратная к часто встречающейся в информатике и математике – там имя одно, а значений у него много. Здесь же ребенок один, а дать имя ему можно любое. Второе – возможность разных ответов к одной задаче в зависимости от контекста, созданного самим ребенком, решающим задачу. Тем самым появление задачи «демистифицируется», т. е. задача берется не с небес, не из задачников и министерских инструкций, а возникает здесь же. Ты сам ее создал.

Обратите внимание, что имена всех детей в задаче должны быть разными. Вообще на одном чертеже или в одной задаче все имена должны быть разными, иначе имена теряют свое предназначение, поскольку нужный объект становится невозможно однозначно указать.

Конечно, работая с утверждениями, дети должны понимать, что очередь за мороженым – это тоже цепочка. Начало и конец цепочки дети должны определить сами. Ясно, что очередь начинается около продавца, ведь человек, который стоит прямо около продавца, купит мороженое первым (он первый в очереди). При вписывании имен в окно кто-то из детей, возможно, будет учитывать и продавца. Однако, продавец не стоит в очереди.

Задача 83. Необязательная. Задача на повторение темы «Одинаковые фигурки». Ребятам, которые совсем запутались можно, как обычно, предложить использовать метод перебора и пометки.

Компьютерный урок «Раньше – позже. Если бусина не одна. Если бусины нет»

Решение задач 96 – 103

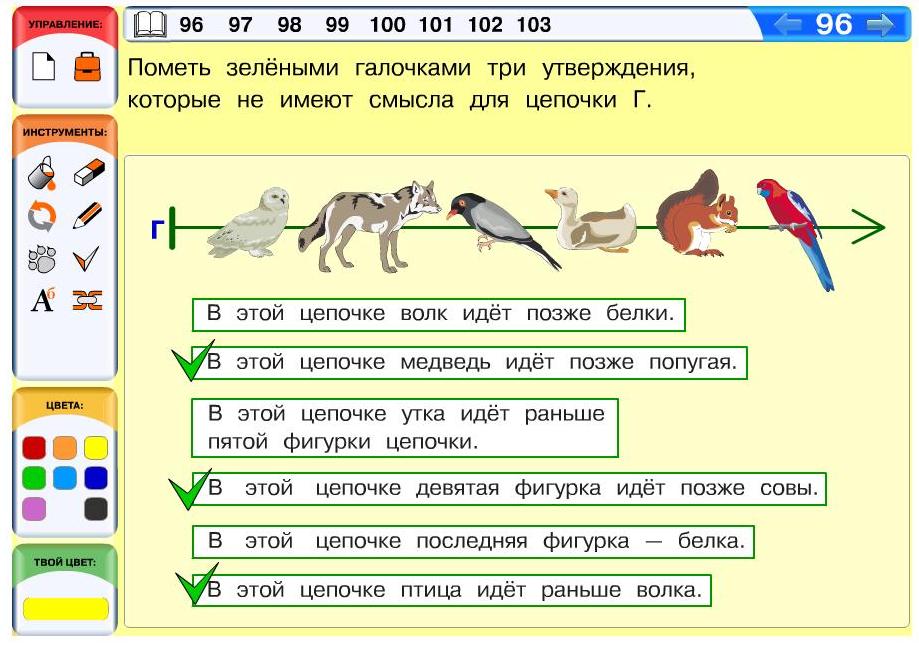
Задача 96. Данная задача напоминает компьютерную задачу 72 из урока «Если бусина не одна. Если бусины нет», только здесь использованы понятия «раньше», «позже». Из данных утверждений не имеют смысла ровно три – второе (в цепочке нет медведя), четвертое (в цепочке нет девятой фигурки), последнее (в цепочке не одна птица).

Задача 97. Если учащийся испытывает сложности в этой задаче, убедитесь, что он понимает причину бессмысленности данного утверждения для данной цепочки. Здесь утверждение не имеет смысла, поскольку в цепочке два дубовых листа. Значит, для того, чтобы утверждение имело смысл, достаточно вынуть из цепочки один дубовый лист.

Задача 98. Нам важно, чтобы у ребят сформировалось понимание того, что для истинности (как и ложности) утверждения необходимо, чтобы утверждение имело смысл. В данном случае для того, чтобы утверждение для некоторого слова имело смысл нужно, чтобы в этом слове была ровно одна буква Е и ровно одна буква Ч. Так данное утверждение не имеет смысла для слов: ЧУДО (нет буквы Е), КУЛАЧОК (нет буквы Е), ЧЕТВЕРГ (две буквы Е), ЧЕЧЕВИЦА (две буквы Е и две буквы Ч). После выполнения первого задания большинство ребят наверняка сообразят, что слова, для которых утверждение истинно, стоит искать не среди всех слов, а среди слов, которые обведены синим.

Задача 99. После знакомства с текущим листом определений ребята должны понимать, что в искомой цепочке должно быть ровно по одной бусине каждого вида, упомянутого в утверждениях: красной квадратной, синей круглой, желтой треугольной, красной круглой. Что касается других видов бусин, они могут быть или не быть в цепочке, причем в любых количествах. Конечно, подходящих решений в этой задаче довольно много.

Задача 100. Здесь продолжается серия задач, посвященных расстановке букв в алфавитном порядке (см. комментарий к компьютерной задаче 83). Первой в этой серии была задача 83. В ней дети расставляли в алфавитном порядке буквы начального фрагмента русской алфавитной цепочки. В этой задаче ситуация немного сложнее – выбраны буквы идущие в алфавитной цепочке подряд, но фрагмент начинается не с начала алфавита (не с буквы А). Однако дети, которые затрудняются в решении, могут по-прежнему начинать перебор с начала алфавита, то есть искать среди данных букв сначала А, потом Б, затем В и т. д., пока они не дойдут по первой по счету буквы в алфавитной цепочке, которая есть в этой задаче. Это буква И, она будет стоять в нашей цепочке первой, поскольку она идет в алфавите раньше всех остальных данный в задаче букв. Продолжаем перебирать алфавит дальше, после буквы И в алфавитной цепочке идет Й. Среди данных в задаче букв Й тоже есть, значит эту букву нужно поставить в цепочку второй. Дальше будет идти буква К, потом Л и т. д. как в алфавитной цепочке вплоть до буквы Р.

Задача 101. Задача на закрепление алгоритма подсчета областей картинки. Как обычно, фрагменты картинки, раскрашенные черным, мы не считаем – они в картинках считаются не областями, а линиями. Здесь картинка довольно сложная и областей много, поэтому дети должны в точности следовать алгоритму подсчета областей.

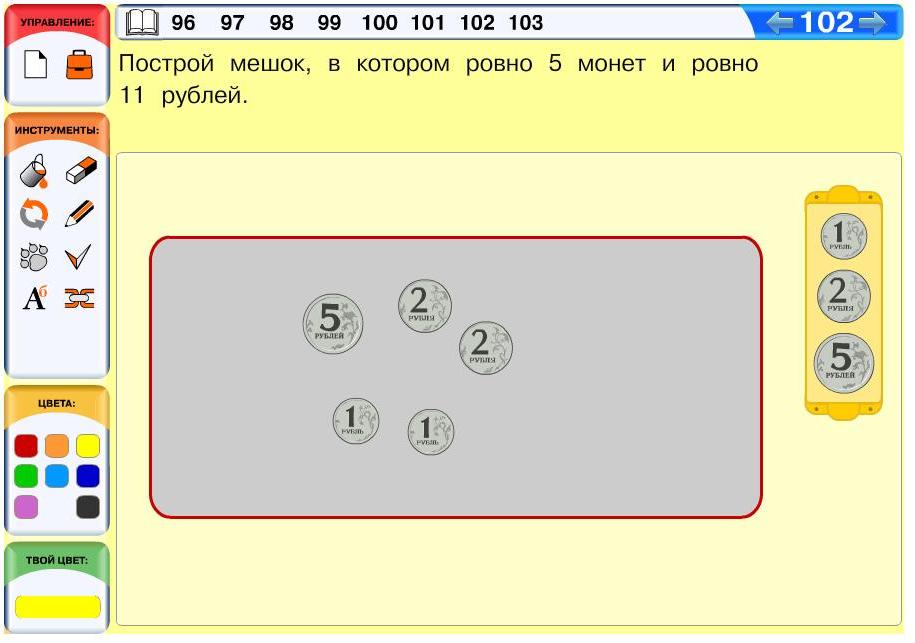
Задача 102. В подобных задачах полезные для решения выводы можно получить либо с помощью рассуждений, либо в ходе проб. Так сумму 11 рублей можно получить, если положить в мешок 11 рублевых монет, но тогда в мешке будет слишком много монет. Можно попробовать вынимать монеты по две и заменять их на одну двухрублевую монету (это постепенно будет уменьшать число монет). Но даже если мы все пары монет заменим на двухрублевые, у нас получается 6 монет – 5 двухрублевых и 1 рублевая. Так мы понимаем, что не получится построить решение без пятирублевой монеты. Несложно понять, что с двумя пятирублевыми моментами решение тоже не построить. Итак, начинаем сначала – положим в мешок одну пятирублевую монету и добавим в него столько рублевых монет, чтобы в мешке оказалось 11 рублей. В мешке стало 7 монет. Это слишком много. Снова начинаем заменять пары рублевых монет монетами в 2 рубля. В этот раз решение удается построить – в мешке у нас будет лежать: 1 пятирублевая монета, 2 двухрублевые монеты и 2 рублевые монеты.

Задача 103. Необязательная. Решать эту задачу можно по-разному, почти любая аргументированная стратегия здесь приведет нас к ответу, даже если мы пока не будем принимать во внимание, что в каждом мешке должно быть по 6 фигурок, а просто попытаемся сделать все мешки одинаковыми. Например, в первом мешке есть помидор, значит, в остальных мешках должен лежать помидор. Добавим помидор во второй и четвертый мешок (в третьем мешке он уже есть). Также в первом мешке есть два ананаса, положим во второй мешок два ананаса, а в третий и четвертый мешок – по одному ананасу (по одному ананасу в них уже есть). Теперь рассмотрим фигурки второго мешка. В нем есть баклажан и редиска, которых нет в других мешках. Добавим в остальные мешки баклажан и редиску. Далее перейдем к третьему мешку, видим, что в первый и второй мешок необходимо добавить цветную капусту. После этого оказывается, что все мешки стали одинаковыми, причем в каждом ровно по 6 фигурок.