Информатика. 2 класс Демо+методичка

Урок 11. «Раньше – позже»

Последовательности

Цепочки – это конечные последовательности, часто используемые в фундаментальной информатике и математике. В обычной жизни наиболее важные последовательности – это последовательности (цепочки) событий или последовательности, связанные с цепочками событий. Но в жизни и деятельности человека встречаются не только временные, но и пространственные цепочки (например, липовая аллея, дома вдоль улицы, всевозможные очереди, гирлянды и бусы).

Когда мы описываем на бумаге временнýю  цепочку событий, у нас возникает новая цепочка – цепочка глав в рассказе или цепочка отдельных предложений, отвечающих событиям. Разбиение слитной речи говорящего на слова и запись этих слов на бумаге еще один пример перехода от временной цепочки к цепочке символов.

Важнейшим отношением между объектами, находящимися в цепочке, является их взаимное расположение. Для описания такого расположения в русском языке используются термины, связанные либо с временнóй, событийной природой важнейших цепочек, либо с пространственной природой отдельных важных цепочек и их моделей на бумаге.

Возникают следующие терминологические возможности:

Бусина А стоит/идёт/встречается впереди/ближе/раньше бусины Б.

Трудность с выражением впереди бусины Б (и аналогичная трудность с выражением перед бусиной Б) связана с тем, что это выражение часто используется и в смысле где-то впереди (как мы и хотим), и в смысле непосредственно, сразу перед («Кто стоит перед тобой в очереди?», «Кто впереди тебя?»). Чтобы избежать возникающей в связи с этим двусмысленности, мы предлагаем пользоваться термином раньше.

Что касается глаголов, то термины стоит, идет и встречается выглядят равнозначными. Мы будем использовать термин идет чаще других.

Обратите внимание, что мы, просматривая некоторую статическую совокупность объектов, скажем, домов на улице или букв в алфавите, говорим: «Булочная идет раньше гастронома» или «В русском алфавите буква К идет раньше буквы П».

Решение задач из учебника

Задача 68 на понимание материала листа определений. Лучше, если дети решат ее самостоятельно. Затем можно устроить фронтальную проверку с обсуждением утверждений, в которых допущено больше всего ошибок. Здесь четвертое утверждение ложное, а остальные – истинные.

Задача 69. Пока мы умышленно избегаем ситуаций, в которых утверждения со словами «раньше/позже» не имеют смысла (такие случаи будут рассмотрены на следующем уроке). Поэтому в каждом слове в этой задаче имеется ровно одна буква Е и ровно одна буква В. В результате при анализе утверждения нетрудно понять, что все слова с первой буквой В нам не подходят, а все слова с первой Е, наоборот, подходят. Таким образом, более внимательно требуется проверить только два слова – ПЕРВЫЙ и НЕРВЫ.

Задача 70. Утверждение не имеет смысла в этой задаче для 5 фигурок, всех фигурок, у которых нет колес.

Задача 71. Здесь нужно проанализировать утверждения и затем вырезать 4 подходящие бусины из листа вырезания. После этого можно начинать выкладывать бусины на столе в цепочку так, чтобы утверждения были истинными. В данном случае задача имеет несколько решений.

Задача 72. Задача на определение истинности утверждений об алфавитной цепочке. Вполне допустимо решать ее, перебирая буквы в уме, а можно решать с опорой в виде алфавитной цепочки с листа определений (стр. 31). В данном случае ровно два утверждения истинны, остальные – ложны.

Задача 73. Необязательная. В этой задаче детям необходимо помнить, что зеркально симметричные фигурки являются разными. 

Компьютерный урок «Раньше – позже»

Решение задач 88 – 95

Задача 88. В этой задаче нет ни бессмысленных утверждений, ни утверждений неизвестно истинных или ложных, что упрощает задачу. Возможно, некоторые дети обратят внимание на четвертое утверждение, оно истинно для любой цепочки, где есть третья и пятая фигурки.

Задача 89. Если кто-то из ребят запутается при решении этой задачи, предложите ему сначала поработать с каждым утверждением в отдельности. Для этого нужно пометить в цепочке луковицу, например, обвести ее. Затем нужно  пометить галочками все фигурки, которые идут в цепочке позже луковицы. После этого нужно обвести лимон и пометить галочками все фигурки, которые идут в цепочке раньше лимона. Фигурки, которые оказались помеченными дважды, нужно раскрасить красным.

Задача 90. Обратите внимание на то, что задание «переставь бусины лапкой», означает, что бусины нельзя вынимать из цепочки, можно только менять их порядок в цепочке. Если дети начнут вынимать бусины из цепочки, утверждения могут потерять смысл.

В этой задаче можно работать с каждым утверждением в отдельности. Наибольшая сложность при этом заключается в том, чтобы работая с некоторой парой бусин, не менять порядок остальных. Первое утверждение для данной цепочки ложно. Чтобы оно стало истинным, достаточно поменять желтую и красную бусины местами. Аналогично, чтобы сделать второе утверждение истинным, нужно поменять местами синюю и зеленую бусины. После этого фиолетовую бусину нужно поставить раньше синей. Конечно, закончить решение нужно как обычно проверкой истинности всех утверждений для получившейся цепочки.

Задача 91. Задача на повторение понятий, связанных с порядком элементов в цепочке, как от начала, так и с конца и их связи. Например, в ходе решения данной задачи ребятам предстоит понять, что пятая с конца бусина здесь является также и первой.

Задача 92. Стратегии решения здесь могут быть разными. Одна из них –  – проверить вначале для всех слов одно из утверждений, вычеркнуть неподходящие слова, а затем для оставшихся слов проверить другое утверждение. Конечно, самые сильные дети при этом догадаются, что более рационально сначала для всех слов проверить второе утверждение (оно позволяет отбросить больше слов). В результате проверки второго утверждения для всех слов остаются не вычеркнутыми ровно 3 слова: САМ, САМОЛЁТ, САЖАЕМ. Поскольку буква С во всех этих словах идет первой, то первое утверждение для всех этих слов тоже буде истинным.

Задача 93. Если кто-то из ребят в этой задаче будет испытывать существенные трудности, предложите ему воспользоваться готовой алфавитной цепочкой. При этом сначала учащийся должен построить свой вариант цепочки, а уже потом обращаться к справочному материалу. Вариант решения, когда ребенок просто впечатывает буквы с готовой цепочки, никакой пользы учащемуся не принесет.

Задача 94. Заметим, что непустых мешков, соответствующих условию, имеется ровно 7.  Действительно, из трех фигурок такой мешок можно составить только один (ведь у нас имеется всего 3 разные фигурки), из одной фигурки – 3 таких мешка, из двух фигурок – тоже 3 мешка. С точки зрения формальной логики и введенного в курсе понятия «все разные» по условию подходит и пустой мешок, ведь в нем тоже нет двух одинаковых фигурок, но вряд ли кто-то из ребят будет использовать в решении пустой мешок.

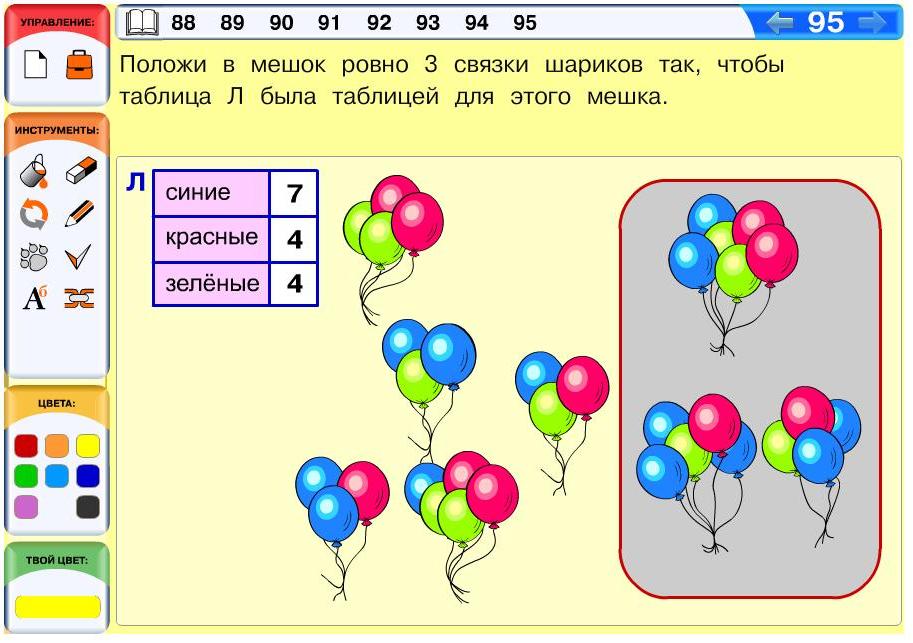
Задача 95. Необязательная. Если у учащегося не появилось никаких идей, он может начать решение методом проб и ошибок, в ходе этой деятельности получая представления о том, каким должно быть решение. Кто-то из детей сразу догадается посчитать общее число шариков в таблице и соответственно в мешке. В мешке должно быть 15 шариков в трех связках. Анализируя количество шариков в имеющихся связках (или в ходе проб), мы понимаем, что не удастся построить решение, не используя связку из 6 шариков, так что ее можно сразу положить в мешок. К ней необходимо добавить 9 шариков, значит одну связку из 5 шариков и одну – из 4 шариков. Синих шариков в таблице существенно больше, чем красных или зеленых, значит логично выбрать связку из 5 шариков, в которой 3 синих шарика. Оставшуюся связку нетрудно подобрать по тому, каких шариков из таблицы в мешке не хватает.