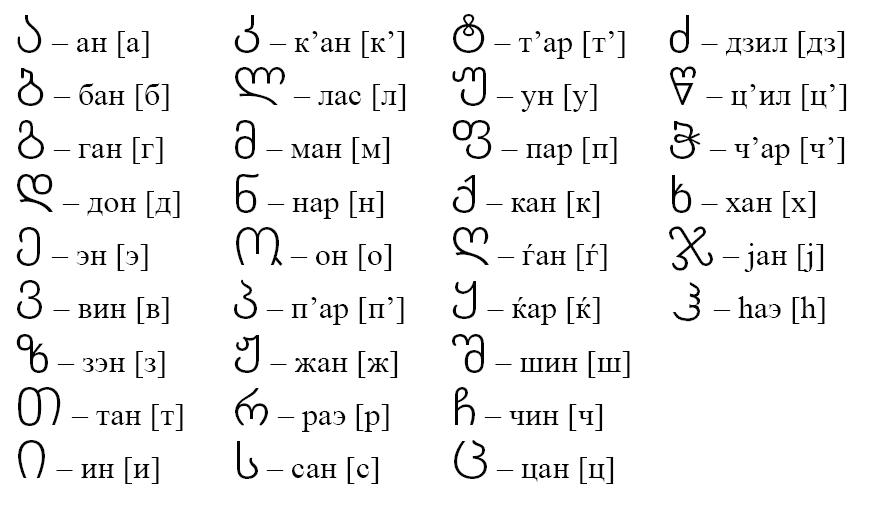Информатика. 2 класс Демо+методичка

Урок 10. «Русская алфавитная цепочка»

Алфавит

Говоря об алфавите, мы обычно имеем в виду две вещи: алфавит как множество (мешок) символов и алфавит как упорядоченная последовательность (цепочка) символов. Необходимость алфавита как множества букв ясна – эти символы используются для коммуникации, для записи человеческой речи. Алфавитная цепочка нам нужна, чтобы было проще искать слово среди других. Представьте себе, что для поиска правильного написания или перевода слова требовалось бы отыскать это слово в мешке, где лежит еще несколько тысяч слов. Как это сделать? На помощь приходит алфавитный порядок. Попробуйте посчитать, сколько страниц вам приходится открыть и сколько слов просмотреть при поиске нужного слова в словаре. Как быстро вы отыскиваете фамилию учащегося в журнале, сколько фамилий вам приходится просмотреть? Обратите внимание на следующие обстоятельства:

1. умение искать слова в цепочках, упорядоченных по алфавиту, является важным жизненным умением – элементом информационной культуры и технологии;
2. деятельность по поиску слова в словаре есть частный случай среди многих видов поиска;
3. детям в школе обычно приходится сначала выучить алфавитный порядок даже без объяснения, зачем это нужно; лишь потом, позднее, они начинают использовать данное умение.

Кстати, проверьте, все ли дети делают правильное ударение в слове алфавит – на последнем слоге.

Лист определений «Русская алфавитная цепочка»

На первый взгляд может показаться, что этот лист определений просто дублирует материал курса русского языка. Но у нас другие цели. Первая – явное и ясное введение всех правил игры. Так, понятие русский алфавит в нашем курсе четко разделяется на два разных понятия – русские буквы и русская алфавитная цепочка. Вторая цель листа определений – показать практические приложения основного понятия курса цепочка. Конечно, в жизни ребенка встречается много важных цепочек – натуральные числа, дни недели, месяцы, расписание и т. д., этот список можно еще долго продолжать. Чем больше таких примеров ребенок осознает и воспримет, тем лучше он усвоит понятие цепочка, с одной стороны, и тем более успешно он будет работать с цепочками в реальной жизни, – с другой.

Алфавитная линейка, как и любая линейка, используется в курсе как инструмент. В частности, ее удобнее, чем алфавитную цепочку, использовать при решении задач.

Решение задач из учебника

Задача 59. В этой задаче дети отвечают на вопросы о русском алфавите (русской алфавитной цепочке). Большинство ребят будет в качестве справочного материала использовать цепочку (или линейку) с листа определений. Действительно, в настоящий момент ребята знают, что первая буква в русском алфавите – А (последняя – буква Я), умеют перечислять буквы в алфавитном порядке. Но далеко не все смогут назвать седьмую букву сразу, для этого детям приходится проговаривать алфавит про себя и одновременно нумеровать буквы, что иногда приводит к ошибкам. Поэтому не надо побуждать детей выполнять все задания в уме – они сами откажутся от визуальной опоры в виде алфавитной цепочки, когда будут к этому готовы.

Задача 60. Для начала необходимо внимательно прочитать условие задачи и понять, что же здесь требуется. Мы здесь должны соединить слово (целиком) с буквой на алфавитной линейке, такой же как третья буква этого слова. Поэтому соединительную линию здесь можно вести так, как это удобно – к букве на левой части линейки от начала слова, к букве на правой части линейки – от конца слова. В данном наборе есть группы слов, имеющих одну и ту же третью букву. Поэтому требуется некоторая аккуратность, чтобы решение было понятно. Слабые дети в этой задаче могут запутаться, поскольку будут соскальзывать с нужной буквы. Таким ребятам можно посоветовать сразу обвести красным третью буквы всех слов, чтобы не забывать на какие буквы смотреть.

Задача 61. Необязательная. Большинство ребят будут действовать в этой задаче методом проб и ошибок, главное при этом не забыть, что бусин должно быть 4. Первое утверждение учесть сразу легко. Переходим ко второму – в нем написано, что после зелёной круглой в цепочке стоит квадратная бусина. Значит, они должны стоят перед треугольной бусиной.  Треугольная бусина – вторая с конца значит, за ней должна стоять еще одна любая бусина. Таким образом, данная задача имеет несколько решений.

Задача 62. Здесь вначале можно пометить (обвести или соединить в пары) все общие бусины, которые есть в обоих мешках. После этого надо нарисовать в первом мешке все бусины, оставшиеся непомеченными во втором мешке, а во втором – все бусины оставшиеся непомеченными в первом мешке. Теперь нужно добавить в мешки одинаковые бусины так, чтобы в каждом мешке стало 7 бусин.

Задача 63. Задача эта технически сложная и может потребовать значительных усилий и от учащихся, и от учителя. Возможны различные ситуации. Например, учащийся быстро нашел пару букв и говорит, что проверил, что их действительно нет. На бумаге при этом не видно никаких следов деятельности, кроме правильно вписанных в окошки букв. Обсудите с учащимся, как он проверял свое решение. Будет хорошо, если он при вашей поддержке изложит (и, возможно, изобретет) какую-либо процедуру, например вычеркивание букв из алфавитной линейки или соединение их с такими же буквами в цепочке и т. п. Это и будет проверкой.

Другая ситуация – учащийся изобрел некоторую регулярную процедуру, но запутался и не смог довести ее до конца. Помогите ему, выступите в роли исполнителя его указаний по решению задачи. Пусть он вас проверит в конце. Вариантов множество. Главное, не забывайте о самостоятельном открытии ребенком собственных подходов к решению задачи.

Задача 64. В случае возникновения ошибок обсудите с ребенком алгоритм решения (и проверки). Первой бусиной в шапке таблицы стоит желтая роза. Сосчитаем, сколько в мешке желтых роз. Для этого сначала пометим все желтые розы в мешке, например красными галочками. После того как все желтые розы будут сосчитаны и число записано в таблицу, переходим к следующей клетке шапки таблицы. Некоторых фигур и шапки таблицы в мешке нет, пишем в соответствующей клетке нуль и двигаемся дальше. Так мы действуем до тех пор, пока не закончатся клетки в шапке таблицы. При этом все фигурки в мешке должны оказаться помеченными.

Задача 65. Необязательная. В этой задаче условию удовлетворяет ровно 5 слов – все слова первого столбца и слово ТОЛЬКО.

Задача 66. Необязательная. В задаче использованы грузинские буквы.

Поскольку необходимо найти все объекты, соответствующие условию, нужно провести полный перебор всех букв. Если учащийся при этом запутался, посоветуйте ему использовать пометки.

Задача 67. Необязательная. Задача на повторение темы «Подсчет областей картинки». Цель данной задачи не просто получить правильный ответ, но и повторить общий алгоритм подсчета областей. Поэтому кроме ответа в окне, в решении должны присутствовать раскрашенные клетки числовой линейки и раскрашенная в соответствующие цвета картинка.

Ответ: в этой картинке 9 областей.

Компьютерный урок «Русская алфавитная цепочка»

Решение задач 80 – 87

Задача 80. Здесь в ходе выполнения инструкции ребята учатся применять понятия, относящиеся к порядку элементов в цепочке, по отношению к русской алфавитной цепочке. Поскольку буквы сравнительно небольшие, некоторым ребятам трудно будет их обвести, не задевая соседние буквы. Задевать другие буквы в целом допустимо, но при этом все-таки должно быть ясно видно, какая буква обведена.

Задача 81. В этой задаче ребята достраивают русскую алфавитную цепочку с помощью «лапки». Наверняка, большинство детей будут восстанавливать цепочку по памяти, повторяя алфавит вслух или про себя. Если вы видите, что слабые учащиеся испытывают в этой задаче сложности, посоветуйте им использовать в качестве справочного материала цепочку с листа определений.

Задача 82. Как и в предыдущей задаче, здесь вполне допустимо, если кто-то из учащихся будет пользоваться алфавитной цепочкой при решении, и даже желательно, чтобы ребята использовали алфавитную цепочку при проверке. Особенно полезна будет алфавитная цепочка в тех утверждениях, где приходится отсчитывать буквы от конца цепочки, ведь даже те дети, которые знают алфавитную цепочку очень хорошо, вряд ли также хорошо воспроизводят ее в обратном порядке.

Задача 83. Словосочетание «буквы стоят в алфавитном порядке» мы будет употреблять в том случае, если буквы расставлены в цепочку в том же порядке, в котором они стоят в алфавите. Это означает, что та буква, которая идет раньше всех остальных в алфавитной цепочке, идет в цепочке первой, буква, которая идет раньше из всех оставшихся, идет второй и т. д. . В данной задаче дети работают с наиболее простым набором букв, поэтому пояснения им вряд ли потребуются (однако будьте готовы их дать). Здесь приведены буквы из начального фрагмента алфавитной цепочки, причем буквы даны подряд, без пропусков. Это означает, что данные буквы будут стоять не просто в том же частичном порядке (то есть между собой), но и на тех же местах, что и в алфавитной цепочке. Первая буква русской алфавитной цепочки – А. Она есть в нашем наборе, ставим ее в цепочку первой, затем в алфавитной и в нашей цепочке будет стоять буква Б, потом В и т. д. до тех пор, пока буквы в нашем наборе не закончатся.

Задача 84. В этой задаче дети повторяют алгоритм подсчета областей картинки. В данном случае картинка довольно затейливая и выделить в ней области визуально оказывается довольно трудно. Тем не менее, сильным учащимся эту задачу лучше предложить сначала на бумаге, а уже после – на компьютере, в качестве проверки.

Задача 85. Здесь учащиеся повторяют понятие «одинаковые цепочки». Поскольку цепочек здесь не много, большинству ребят удастся найти две одинаковые цепочки хаотичным просматриванием.

Задача 86. В этой задаче мы ведем пропедевтику операций над множествами (а мешки здесь являются множествами). Знаки, которые необходимо найти и пометить в задаче, составляют пересечение множеств А и Б. Это знаки, которые есть в каждом из двух множеств. В данном случае таких знаков оказывается всего 3. Обратите внимание, в данном случае общие знаки нужно пометить только в мешке А.

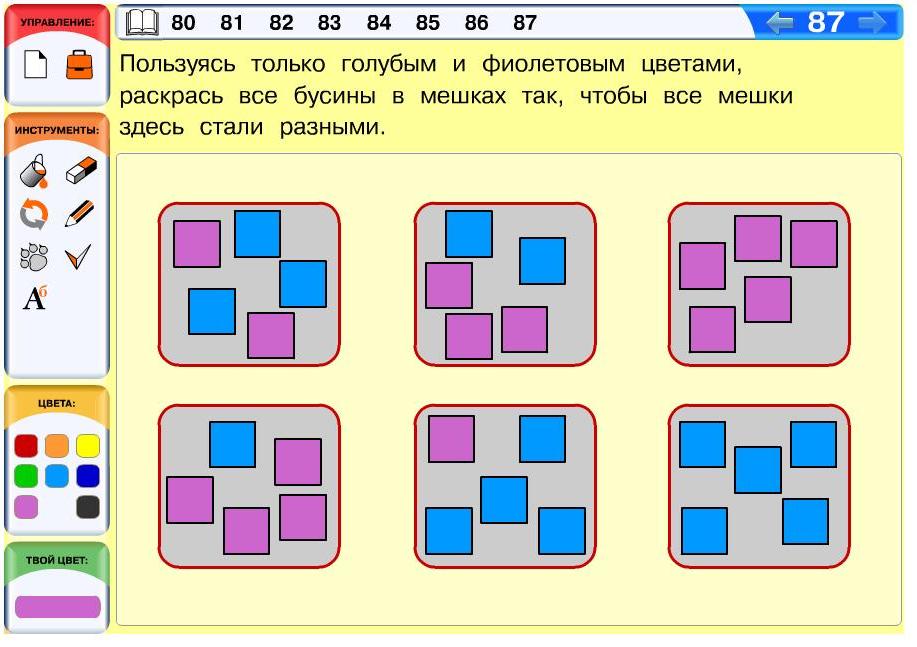
Задача 87. Необязательная. Решение здесь можно построить как методом проб и ошибок, так и используя рассуждения. Действительно, все бусины в каждом мешке должны быть раскрашены в два цвета. Это означает, что бусины, которые не будут раскрашены голубым, нужно будет раскрасить фиолетовым и наоборот. При этом все бусины в мешках одинаковой формы, значит, мешки можно сделать разными только за счет цветов бусин. Из всего сказанного можно сделать вывод, что мешки будут полностью определяться числом голубых бусин в них, а оно может быть от 0 до 4.