Информатика. 2 класс Демо+методичка

Урок 7. «Отсчитываем бусины от конца цепочки»

На этом уроке ребята продолжают знакомиться с понятиями, характеризующими порядок элементов в цепочке. Учащиеся уже знают, что бусины в цепочке можно нумеровать от начала: первая, вторая, третья и т. д. На этом уроке дети узнают, что аналогично можно нумеровать бусины и от конца: первая с конца, вторая с конца, третья с конца и т. д. . Заметим, что учащиеся уже знакомы с двумя понятиями, касающимися нумерации элементов от конца цепочки – последний и предпоследний. В ходе решения задач по данной теме ребятам придется состыковать новые понятия с уже изученными, в частности, учащимся предстоит понять, что первая с конца фигурка – то же самое, что последняя, а вторая с конца – то же, что предпоследняя.

Решение задач из учебника

Задача 44. Задача на понимание материала листа определений. При возникновении затруднений с определением истинности какого-то из утверждений, попросите учащегося выделить бусины, о которых в нем идет речь. Например, при работе с первым утверждением нужно найти в цепочке вторую бусину и третью с конца бусину. Среди данных утверждений ровно одно ложное утверждение, а остальные – истинные.

Задача 45. Здесь дети впервые в курсе 2 класса выполняют инструкцию. Проверьте, все ли ребята помнят, что пункты инструкции должны выполняться строго друг за другом в порядке, указанном нумерацией. Если учащийся ошибся при выполнении одного из пунктов, может случиться, что один из следующих пунктов он выполнить просто не сможет (поскольку нужная бусина уже раскрашена). Ребята в этом случае должны понимать, что необходимо вернуться к началу инструкции и все еще раз проверить.

Задача 46. На примере этой задачи ребята могут убедиться, что нумерации элементов цепочки от начала и с конца могут быть связаны по-разному. Так в данном случае условию задачи удовлетворяют 5 слов, причем в двух из них третья буква с конца является также и третьей с начала, а в двух – эта буква стоит первой.

Задача 47. Это задача на перебор вариантов, по сути, она комбинаторная. Все цепочки в задаче изначально одинаковые, а их нужно сделать разными. Попробуем сделать это, раскрашивая бусины по порядку, используя два цвета. Первая бусина цепочек может быть оранжевой или зеленой. Цвета для нас совершенно равнозначны, значит можно в двух цепочках раскрасить первую бусину оранжевым, а в других двух – зеленым. Ясно, что ни одна из цепочек с первой зеленой бусиной не может быть такой же, как одна из цепочек с первой оранжевой бусиной, поэтому дальше можно рассматривать цепочки только в парах. Впрочем, дети, наверняка без всяких рассуждений смогут докрасить цепочки по-разному, пользуясь методом проб и ошибок, поскольку в небольшом наборе объектов не так легко запутаться. Чтобы у детей не возникло проблем с исправлением ошибочных решений, можно посоветовать им, сначала не закрашивать бусины полностью, а лишь отметить их выбранным цветом. После того как ребенок убедится, что все цепочки действительно разные, он может раскрасить бусины полностью.

Задача 48. Необязательная. В этой задаче сразу бросается в глаза, что красный квадратик есть во всех фигурках, зеленый только в пяти. Теперь остается проверить, в каких из этих 5 фигурок нет синего квадратика.

Задача 49. Необязательная. Здесь много «пар-ловушек» – цепочек, которые очень похожи, но не одинаковы. В этой задаче вполне вероятно, что многие дети допустят ошибки. В таких случаях нужно попросить внимательно проверить решение, сопоставляя бусины на соответствующих местах, найти ошибку, а затем отыскать верное решение.

Задача 50. Конечно же, мы имеем дело с цепочкой. Трудность в том, какую книжку считать началом цепочки – верхнюю или ту, что Миша положил на стол первой. Формулировка утверждений подсказывает нам, что начало цепочки – словарь, а конец – букварь. Однако кто-то из детей, возможно, будет путаться с этим. Самый простой выход в такой ситуации – взять несколько книг и выложить их стопкой на стол. Из данных утверждений первое утверждение истинно, а остальные – ложные.

Задача 51. Необязательная. В отличие от предыдущей задачи здесь все утверждения такие, о которых неизвестно, истинные они или ложные. Детям это может показаться странным, но в жизни такие ситуации встречаются достаточно часто.

Компьютерный урок «Отсчитываем бусины от конца цепочки», 1 часть

Решение задач 56 – 63

Задача 56. В целом задача аналогична задаче 44 из учебника. В случае ошибок попросите учащегося выделить ту фигурку или фигурки, о которых идет речь в утверждении. Что касается второго утверждения, большинство детей, скорее всего, определит его как неизвестно истинное или ложное. Если среди ваших детей окажется знаток рыб, который скажет вам, что эта рыба не карась и предоставит какие-либо аргументы, то ребенок может определить утверждение как ложное. Недопустимо здесь только пометить второе утверждение как истинное, поскольку написанное в нем неверно.

Задача 57. Кроме хаотичного просматривания здесь можно воспользоваться одной из двух стратегий. Первая состоит в том, чтобы по очереди просматривать цепочки и для каждой определять истинность обоих утверждений. Вторая состоит в том, чтобы сначала для всех цепочек проверить первое условие (и все неподходящие цепочки вычеркнуть), а затем для оставшихся цепочек проверить второе условие. Вторая стратегия позволит закончить перебор несколько быстрее. Действительно, лишь в двух цепочках третья бусина с конца квадратная. Только для этих цепочек есть смысл проверять второе условие.

Задача 58. На примере данной задачи дети могут заметить, что последняя бусина и первая с конца – это одно и то же. Если кто-то из ребят допустил в этой задаче ошибки, попросите его сначала явно сформулировать все условия, которые должны выполняться для цепочки. Затем нужно попросить учащегося пометить в цепочке те бусины, о которых идет речь (третью с конца и последнюю).

Задача 59. Начать здесь лучше с третьего утверждения, поскольку оно определяет одну из фигурок (третью с конца) однозначно. Вторым можно использовать первое утверждение. Третья фигурка в цепочке уже стоит, это зеленый жук, значит в силу первого утверждения вторая фигурка тоже зеленый жук. Теперь понятно, что в силу второго утверждения коричневый жук должен стоять первым. На оставшихся местах помещаем две оставшиеся фигурки. В данном случае задача имеет единственное решение.

Задача 60. Чтобы решить данную задачу, ребята должны понимать значение выражения «есть 4 разные буквы». Это понимание позволяет сразу отбросить часть неподходящих слов. Во-первых, нам не подходят все слова из трех буквы – в них вообще нет четырех букв (СЫР, ПИР). Во-вторых, нам не подходят те слова из четырех букв, в которых есть хотя бы две одинаковые буквы – это противоречит определению понятия «все разные» (ПАПА, МАМА, ПАРА). То есть из четырехбуквенных слов нам подходит лишь два – ДЫРА и ПИСК. Остальные слова надо перебрать более внимательно, для каждого считая число разных букв. Если их хотя бы 4 (или больше), то слово нам подходит. Если – меньше четырех, то не подходит. Например, возьмем слово ТОПОТ. В нем всего 3 разные буквы Т, О и П, значит это слово нам не подходит. Так мы работаем со словами, пока не закончим полный перебор всех слов.

Задача 61. Задача на повторение таблицы для мешка (одномерной). В данном случае дети одновременно будут брать информацию из двух таблиц. Лучше использовать клетки таблиц по очереди. Чтобы не запутаться, использованные клетки таблиц лучше сразу помечать. Например, собираем в мешок сначала квадратные бусины. Их должно быть 5. Смотрим их цвет во второй таблице. Берем одну красную квадратную бусину, помечаем первую клетку второй таблицы. Затем берем 2 оранжевые квадратные бусины, помечаем вторую клетку таблицы. Осталось положить в мешок еще две квадратные бусины, их можно взять зеленого цвета и пометить четвертую клетку таблицы или взять 2 желтых квадратных бусины, а третью желтую бусину взять уже круглой формы. После этого можно пометить первую клетку первой таблицы и т. д.

Задача 62. Задача на построение мешков по описанию. Большинство ребят будут решать ее методом проб и ошибок – в данном случае этот способ является наиболее естественным и достаточно эффективным.

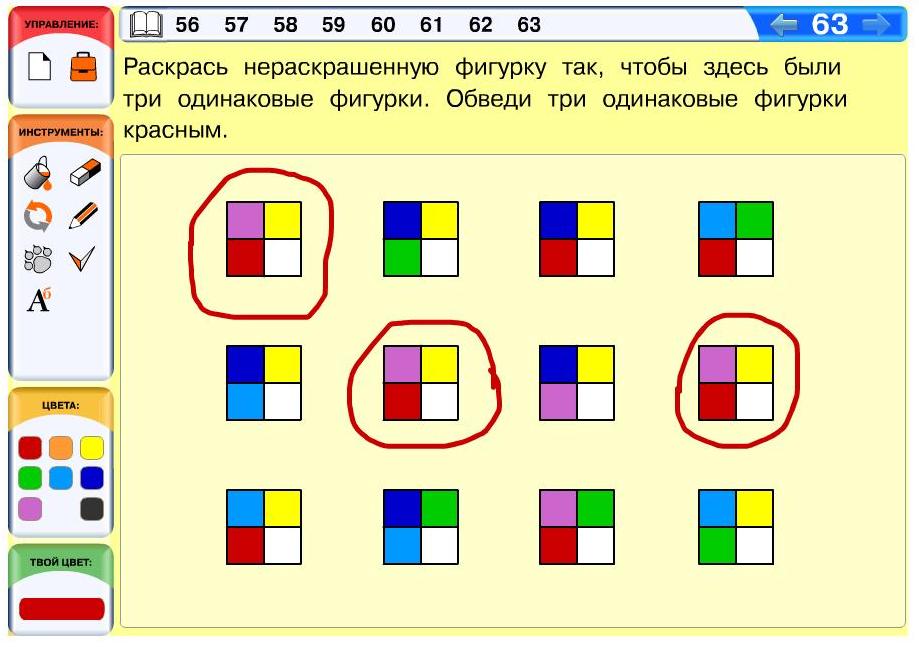
Задача 63. Необязательная. По сути, эта задача интегрирует в себе два типа заданий – «найди две одинаковые фигурки» и «сделай фигурку такой же». Действительно, для того чтобы сделать одинаковыми три фигурки, нужно сначала найти две одинаковых фигурки среди раскрашенных, т.к. раскрасить можно лишь одну фигурку. Поиск двух одинаковых фигурок может происходить несколькими способами. Кто-то, возможно, найдет их хаотическим просматриванием, однако этот процесс может затянуться. Гораздо надежнее полный перебор либо разбиение фигурок на группы по цвету, например, левой верхней клетки. Понятно, что одинаковые фигурки надо искать в пределах каждой группы, сравнивать объекты из разных групп нет никакой необходимости. Одинаковые фигурки – вторая и четвертая слева в среднем ряду.

Компьютерный урок «Отсчитываем бусины от конца цепочки», 2 часть

В этом компьютерном уроке дети знакомятся новым инструментом – конструктором цепочек, который в задачах мы кратко называем «цепочка». Поэтому 2-3 первых задачи данного урока необходимо решить со всем классом обязательно. Из остальных задач вы можете выбрать задачи по своему усмотрению.

Если ребенок хочет начать рисовать цепочку, то он должен выбрать (щелчком мыши) в инструментах «цепочку», а затем щелкнуть в том месте рабочей страницы, где он хочет начать рисовать цепочку. После этого на экране появится пустая цепочка, то есть по сути соединенные вместе начало и конец цепочки. Чтобы поместить в эту цепочку фигурку, нужно взять ее лапкой, например из библиотеки, и наложить на ось цепочки между началом и концом. После этого цепочка раздвинется, и наша фигурка окажется в цепочке. Допустим, мы теперь хотим вставить еще одну фигурку перед той, которую мы уже поместили в цепочку. Тогда надо снова наложить вторую фигурку на ось цепочки между началом и первой фигуркой. Цепочка при этом снова раздвинется, и вторая фигурка окажется снова вставленной в цепочку.

Если ребенок хочет удалить какую-то фигурку из цепочки, это, как обычно, можно сделать ластиком. При этом цепочку можно удалить только пустую. Поэтому, если ребенок нарисовал цепочку, а затем решил удалить ее целиком, проще будет использовать команду «начать сначала». В противном случае фигурки нужно удалять по одной, а затем уже удалять пустую цепочку.

Решение задач 64 – 71

Задача 64. В этой задаче дети впервые пробуют новый инструмент «цепочка». Убедитесь, что все учащиеся поняли, как он работает. В данном случае цепочка по условию должна состоять из одной бусины, причем бусина может быть любой. Поэтому проблема с удалением бусин в этой задаче, скорее всего, не встанет. Если это все-таки произошло, обсудите с учащимися в индивидуальном порядке, какие инструменты он может использовать, чтобы исправить свое решение.

Задача 65. Еще одна задача на использование нового инструмента. Содержательно задача совсем простая, ведь цепочка должна удовлетворять лишь одному условию – состоять из трех бусин. В этой задаче мы обращаем внимание ребят на то, что неправильно нарисованную в цепочке бусину можно стереть ластиком. Вообще-то фигурки в наших задачах ластиком не стираются почти никогда. Исключение составляют фигурки, которые ребенок сам взял в библиотеке. В данном случае это именно так.

Задача 66. Из второго утверждения следует, что в цепочке должно быть не  меньше семи фигурок (в противном случае второе утверждение будет бессмысленным). Из первого утверждения следует, что вторая с конца (предпоследняя) и третья с конца фигурки – одинаковые. Если одна из них оказывается седьмой, значит это одинаковые птицы. Подходящих цепочек в данной задаче много (поэтому решение несложно отыскать методом проб и ошибок). Один из самых простых вариантов – построить цепочку из 7 одинаковых птиц, но конечно дети предложат вам самые разные варианты цепочек.

Задача 67. В случае ошибок, попросите учащегося в каждом слове выделить четвертую букву с конца, например, красной галочкой, а также пометить вторую букву от начала и от конца, например синей галочкой. Если и после этого учащийся не нашел все свои ошибки, нужно проверить, насколько качественно он проводит перебор. В частности, просмотренные слова лучше сразу обводить – если слово подошло, то синим цветом, если не подошло, каким-то другим.

Задача 68. Это интегрированная задача, которая находится на стыке математики, информатики и практической деятельности. Действительно, с точки зрения информатики это задача на построение мешка (кошелька) по описанию. С точки зрения математики для решения задачи необходимы определенные вычислительные навыки, в частности ребенок должен уметь складывать числа в пределах 20. Объекты же в этой задаче практические – монеты, с которыми ребенок имеет дело в своей жизни. Проще всего детям решать такие задачи перебором, который легко вести по самым крупным монетам, в данном случае – пятирублевым. Если мы положим в кошелек 5 пятирублевых монет, то в нем окажется 25 рублей, значит, пятирублевых монет нужно брать меньше. Возьмем 4 пятирублевых монет и 1 двухрублевую, в этом случае в кошельке оказывается 22 рубля, что тоже нам не подходит. Теперь возьмем 3 пятирублевых монеты и 2 двухрублевые, в этом случае в кошельке оказывается 19 рублей, значит, мы построили решение.

Задача 69. Первое утверждение ложно, значит, в этой цепочке нет двух одинаковых фигурок (все фигурки – разные). Второе утверждение ложно, значит в цепочке не меньше 5 бусин (то есть пять или больше). Третье утверждение тоже ложно, значит в цепочке не все фигурки – бабочки (в цепочке есть не бабочки). Слабым детям как обычно можно посоветовать метод проб и ошибок – построить сначала цепочку как-нибудь, а затем для нее проверить три данных утверждения. Если хотя бы одно из них окажется не ложно, то цепочку необходимо подправить.

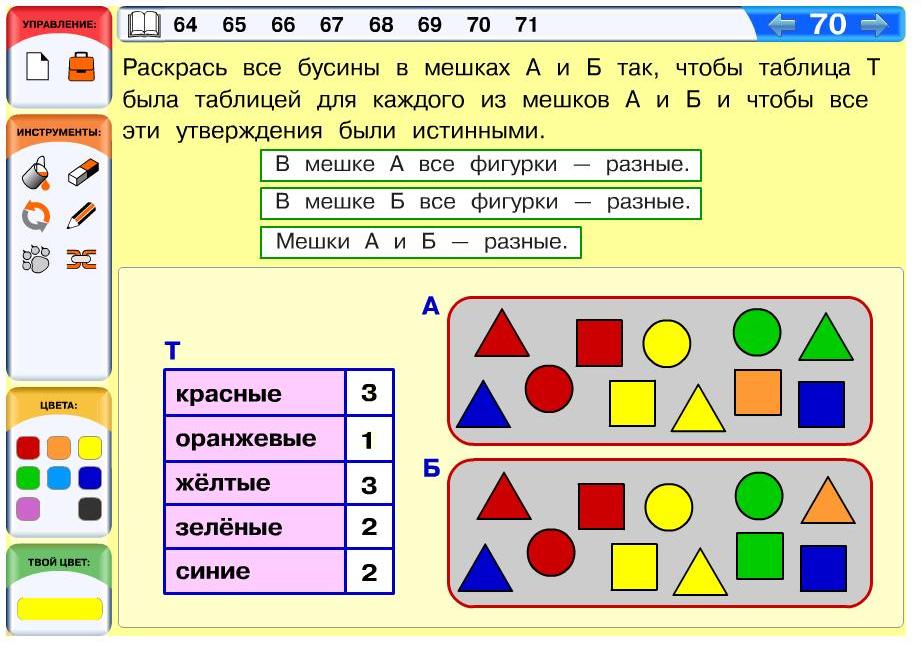
Задача 70. В этой задаче ребята еще раз убеждаются, что далеко не всегда мешок определяется таблицей для мешка однозначно, даже в том случае, когда на этот мешок накладываются дополнительные условия. Если ребенок в этой задаче запутался, попросите его сначала раскрасить по таблице бусины мешка А так, чтобы в нем все бусины стали разными (то есть было истинно первое утверждение). В ходе этой работы ребенку многое станет понятно. Например, в мешке должно быть 3 красные бусины, но при этом в мешке не должно быть одинаковых бусин, значит надо раскрасить красным 3 бусины разной формы – треугольную, квадратную и круглую. Аналогично дело обстоит и с желтыми бусинами, здесь в нас тоже нет выбора. Поэтому лучше всего начинать раскрашивать с тех клеток таблицы, где стоят наибольшие числа, иначе бусин некоторой формы впоследствии может просто не хватить. Раскрасим бусины красным и желтым, а потом, например, зеленым. Здесь у нас уже есть некоторый выбор – можно раскрасить зеленым круглую и квадратную бусину, можно круглую и треугольную или квадратную и треугольную. Именно за счет такой вариативности впоследствии удается сделать мешок Б отличным от мешка А.

Задача 71. Необязательная. Здесь имеется два цвета и в каждой фигурке по 4 нераскрашенных лепестка. Нужно получить при раскрашивании 5 разных вариантов раскрашивания этих лепестков (ведь все остальные лепестки раскрашены одинаково). Вообще-то разных вариантов здесь довольно много. Даже если мы будем раскрашивать всегда ровно два красных и ровно два синих лепестка, то сможем получить уже 6 разных фигурок. Поэтому проводить полный систематический перебор здесь не потребуется. Скорее всего, дети найдут решение случайным перебором, методом проб и ошибок. Поэтому в качестве эксперимента можно попробовать предложить эту задачу даже слабому ребенку, если она его заинтересует.