Информатика. 2 класс Демо+методичка

Урок 5. «Имена»

Присвоение имен – важнейшая функция человеческого мышления и языка. Согласно Священному Писанию еще до сотворения Евы первому человеку было предоставлено право назвать сотворенных Господом животных и птиц:

«Господь Бог образовал из земли всех животных полевых и всех птиц поднебесных и привел их к человеку, чтобы видеть, как он назовет их, и чтобы, как наречет человек всякую душу живую, так и было имя ей».

Замечательный русский поэт второй половины ХХ в. Давид Самойлов писал:

У зим бывают имена. Одна из них звалась Наталья. И были в ней молчанья тайна, И холод, и голубизна...

Понятие имени – одно из важнейших в информатике и математике. Мы в нашем курсе будем давать имена самым разным объектам: цепочкам, фигуркам и пр. Именем может быть любое слово (вспомните наше определение слова как любой цепочки букв) и даже любая цепочка букв и цифр.

В традиционных книгах по информатике и математике часто говорят не об именах и значениях, а о переменных, параметрах, константах и их значениях. Несколько огрубляя ситуацию, можно сказать, что переменные меняют значение часто и их значение во многих случаях неизвестно (вот еще одно слово традиционной математики – неизвестное, мы же употребляем слово неизвестно в обычном смысле). Параметры более постоянны в своих значениях; впрочем, эти значения тоже нам, как правило, неизвестны. Что касается констант, то обычно (но не всегда) их значения действительно постоянны и в общем-то известны, например число π. Вы видите, что ситуация не такая простая, и поэтому мы в начальной школе предпочитаем говорить только об именах.

Часто в математике и особенно в информатике используются имена, не просто являющиеся произвольными цепочками букв, а отражающие использование этих имен: «подлежащее», «время в пути» и т. п.

Сокращения и «вольности речи»

В повседневной жизни люди часто произносят фразы и пишут тексты, которые могут быть поняты по-разному, причем иногда разница в понимании может оказаться весьма существенной. Как правило, в таких случаях слушающему или читающему выбрать из различных пониманий то, которое имеется в виду говорящим или пишущим, помогают какие-то обстоятельства. Если же уверенности нет, то можно задать уточняющий вопрос, спросить, что имеет в виду собеседник. В случае письменного текста можно попытаться перечитать еще раз предшествующий фрагмент или продолжить чтение, рассчитывая на прояснение в дальнейшем.

Причин возникновения неоднозначности в тексте много. Одна из них – стремление к краткости. Полный текст был бы слишком длинным, и говорящий надеется, что его поймут с полуслова. В математике тексты, в особенности, записанные с помощью математических формул, чаще оказываются однозначными, и в данном случае это является важным. Однако и здесь, особенно в неформальной части математических текстов, возникают неоднозначности, но математики заведомо идут на это ради большей краткости и понятности всего текста. Дело в том, что нередко, чтобы достичь однозначности понимания текста и полной точности выражений, приходится делать его очень длинным и громоздким, а значит, трудным для восприятия. Однако при работе с компьютером это часто является необходимым. Возникает проблема: компьютер требует полной однозначности, а человек – если не лаконичности, то по крайней мере обозримости.

Мы уже понимаем, что значат слова цепочка с именем Х или фигурка с именем А. Как мы уже показали, можно говорить и короче: цепочка Х и фигурка А. Проблема возникает в связи с тем, что имена у нас тоже цепочки. Поэтому, когда мы будем говорить цепочка Х, нам придется догадываться, идет речь о цепочке из одной бусины Х или о какой-то другой цепочке с именем Х, может быть состоящей из тысячи бусин. Иногда догадаться будет просто невозможно, и тогда нам придется возвращаться к более точному и более громоздкому выражению цепочка с именем Х.

Решение задач из учебника

Задача 30. Здесь надо только дать имя каждой фигурке. При этом дети могут дать имена, соответствующие характеру фигурок – СНЕГИРЬ, МЯЧ, ЩЕНОК. Также дети могут дать имена в обычном понимании этого слова (языковом) – КЕША, ТОБИК. С другой стороны, кто-то даст фигуркам формальные имена, никак не касающиеся их содержания или внешнего вида – А, НРН, 1А2М и т.д. Все эти варианты вполне допустимы, ведь они соответствуют определению понятия «имя» (как любой цепочки букв и цифр). Какие ошибки могут допустить дети в именовании (присвоении имен)? Мы не можем дать имя из двух слов, например, «БАСКЕТБОЛЬНЫЙ МЯЧ». Это противоречит введенному определению, ведь это уже не одна, а две цепочки. Кроме того, в речи принято имена собственные писать с большой буквы, поэтому кто-то из детей так и напишет «Тобик». В таком случае нужно обратить внимание детей, что в нашем курсе нет заглавных и строчных букв – все буквы одинакового размера (заглавные).

Задача 31. Данная задача дает детям необходимый пример употребления имен. Действительно, зачем нам давать имена (цепочкам или фигуркам)? Когда цепочка одна, это не является столь уж актуальным – ведь мы всегда можем написать «в этой цепочке». Но если цепочек в задаче несколько, а мы хотим указать одну из них, то без имен обходиться трудно. Раньше во многих случаях нас спасала возможность решить задачу графическими способами, тогда можно просто обвести нужную цепочку. Однако, обойтись без имен можно далеко не всегда и чем сложнее задачи, тем это все труднее. В этой задаче введение имен дает ребенку определенный выигрыш по времени, ведь вписать букву в окно гораздо быстрее, чем обвести цепочку.

Задача 32. По содержанию эта задача не сложная.  Как видите, в первое окно можно вписать лишь одно имя – «Д». Соответственно во второе окно можно вписать имя любой из оставшихся цепочек.

Задача 33. Необязательная. Здесь мы даем детям подсказку, как проверить, что выбраны действительно все нужные объекты, – на листе вырезания не должно остаться слонов. Разумеется, в окне не должно оказаться каких-то других фигурок (не слонов). Только при выполнении этих условий решение будет правильным. 

Задача 34. Для решения этой задачи детям необходимо понимание того, что выражение «ровно две буквы Е» подразумевает, что в слове есть две буквы Е, но нет трех букв Е. Например, по условию не подходит слово ПЕРЕЛЕСКИ (в нем 3 буквы Е) или ТРЕУГОЛЬНЫЙ (в нем одна Е).

Задача 35.  В задачах на поиск одинаковых мешков можно использовать разные стратегии. Можно выполнить полный перебор по определенной системе, сравнивая каждый мешок с каждым, но это очень долго. Более удобно – делить мешки на группы, по определенному признаку и дальше сравнивать мешки в группах уже только между собой (это существенно уменьшит число сравнений). Признаки можно выделять разные, например, число фигурок в мешке. В данном случае у нас 5 мешков содержат 6 бусин и 1 мешок (Л) – 5 бусин. Мешок Л можно сразу вычеркнуть, поскольку для него такого же мешка точно нет. Дальше при сравнении оставшихся мешков  нам очень помогает цвет фигурок. Например, сразу видно, что в 4 мешках (М, Н,О,П) есть две зеленые бусины, а в мешке К зеленая бусина одна. Мешок К тоже можно вычеркнуть, а оставшиеся 4 мешка разделить на группы по наличию или отсутствию фиолетовой бусины.

Задача 36. Необязательная. Подобные задачи способны заинтересовать многих детей. Эта задача находится на стыке нашего курса и окружающего мира. С точки зрения информатики это задача на выделение объекта по описанию. А лексика при составлении описания взята частично из окружающего мира (майки, бантики), да и сами фигурки скорее сказочные, чем информатические.

Задача 37. Необязательная. Большинство ваших ребят наверняка знают, что в русском языке имеется ровно 10 гласных букв. Если положить (записать) их все в мешок, то получится мешок, в котором: нет двух одинаковых букв, все буквы гласные, букв ровно 10. Теперь можно убрать одну любую букву из мешка и получится искомый мешок. Таким образом, по описанию, приведенному в данной задаче, можно построить ровно 10 разных мешков.

Компьютерный урок «Имена»

Решение задач 39 – 46

Задача 39. Данную задачу следует считать скорее практической, чем учебной. Действительно, не вся лексика данной задачи входит в правила игры (является лексикой нашего курса), часть лексики взята из обычной речи. Именно поэтому ребенок может не знать слово «манишка». Однако, это не помешает ему решить данную задачу, ведь белый участок окраса есть лишь у одного кота  на рисунке. Кстати «белая» тоже можно считать контекстной лексикой, взятой из обычной речи, ведь в нашем курсе нет белых областей, мы их считаем нераскрашенными. Конечно, по отношению к окрасу кота так говорить не приходится.

Задача 40. Здесь удобнее всего раскрашивать соответствующие бусины цепочек К и Л одновременно, двигаясь от начала цепочек к концу. Затем можно раскрасить бусины цепочки М так, чтобы цепочки К (или Л) и М отличались хотя бы парой бусин, стоящих на одних и тех же местах. Например, достаточно раскрасить первую бусину цепочки М не таким цветом, каким раскрашена первая бусина цепочки К.

Задача 41. Сильные ученики, скорее всего, уже могут проанализировать все три утверждения, состыковать условия описания между собой и строить решение осознанно. Действительно, в силу второго утверждения в цепочке А нет одинаковых фигурок, значит в свободные окна цепочки А нужно поставить петуха и синицу. В свободные окна цепочки Б мы поставим оставшиеся фигурки, тоже петуха и синицу. При этом предпоследняя фигурка цепочки Б – синица, значит петух – третья фигурка цепочки Б. В силу первого утверждения цепочки А и Б должны быть разными, значит в цепочке А третьей фигуркой нужно поставить синицу, а предпоследней – петуха. Слабые учащиеся, которые не смогут построить такие рассуждения с опорой на данные утверждения, будут действовать методом проб и ошибок.

Задача 42. Здесь детям для решения необходимо выполнить полный перебор всех слов. Буква П в каждом из слов стоит первой, это облегчает проверку истинности утверждения.

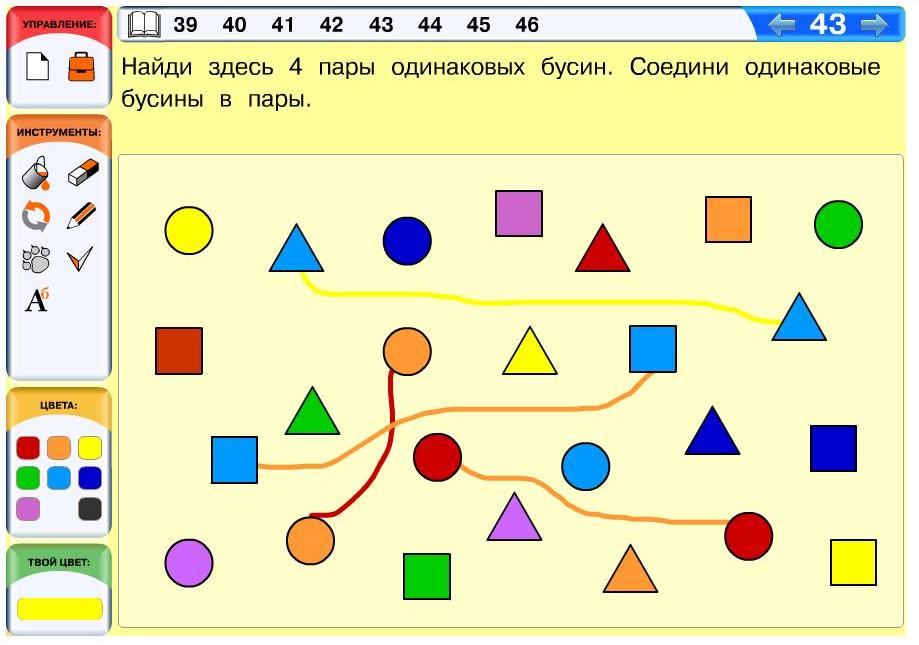
Задача 43. В данном случае нужно найти 4 пары одинаковых бусин, что усложняет задачу. Кто-то из учащихся, чтобы найти все нужные пары, будет использовать перебор, но проще разделить все бусины на группы по цвету и искать одинаковые бусины среди бусин одного цвета. Например, рассмотрим желтые бусины. Их три и все они разные, значит, желтые бусины можно пометить как просмотренные и перейти к бусинам другого цвета, например, оранжевого. Среди оранжевых бусин есть две одинаковые. Соединяем их в пару, а остальные оранжевые бусины помечаем как просмотренные и переходим к следующему цвету. Так действием до тех пор, пока пар одинаковых бусин не наберется четыре.

Задача 44. В курсе 1 класса детям встречалась похожая компьютерная задача (см. комментарий к компьютерной задаче 193 курса 1 класса). Данная задача отличается от задачи 193 наличием имен мешков, которые позволяют кратко указать мешок, о котором идет речь. Нетрудно убедиться, что с именами формулировка такой задачи становится существенно легче для понимания.

Задача 45. В данном случае не все объекты отыскиваются однозначно. Одинаковых фигурок здесь ровно две, любая может быть А или Б. Фигурок с двумя зелеными колечками здесь тоже две, любая из них может быть Г, а оставшаяся будет В. Однозначно определяется здесь только фигурка Д – пирамидка с двумя красными колечками.

Задача 46. Необязательная. В этой задаче ведется пропедевтика понятия «все разные», которое будет введено на следующем уроке. В ходе работы с одинаковыми и разными фигурками ребята уяснили следующее – чтобы в наборе не было одинаковых фигурок нужно, чтобы фигурки одной формы были разных цветов, ведь фигурки разных форм будут разными в любом случае. Поэтому проще всего разбить все фигурки на группы по формам и раскрашивать эти группы по очереди. Например, рассмотрим группу восьмиугольников. В ней осталось 3 нераскрашенные фигурки. Значит, их нужно раскрасить в три разных цвета, но при этом нельзя использовать цвета, которыми уже раскрашены другие восьмиугольники. Значит три нераскрашенные восьмиугольника нужно раскрасить: голубым, фиолетовым и черным цветами.