Информатика. 2 класс Демо+методичка

Урок 3. «Считаем области»

Топология

Математику часто определяли как науку о числах и фигурах. В современной математике роль чисел существенно меньше, как и роль фигур в их классическом понимании. Эти изменения находят отражение в нашем курсе: в нем, в частности, появляются начала топологии – важной и интересной области современной математики. Особое значение топология приобретает в связи с развитием информатики, начиная с проблем топологии интегральных схем и кончая задачами распознавания изображений компьютером.

Чтобы пояснить, чем занимается топология, можно сказать, что она изучает свойства фигур в пространстве, которые сохраняются при непрерывных преобразованиях этого пространства. Но это лишь приблизительное описание, в частности, потому, что математическое понимание пространства тоже не совпадает с нашим обычным пониманием и требует особого пояснения. Сделаем это на следующем примере.

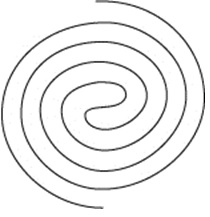
Давайте выберем в качестве пространства воздушный шар, только абстрактный, математический: его можно как угодно растягивать, сжимать, деформировать без всякого сохранения размеров, но не прорывать. Нарисуем на шаре какую-нибудь кривую, опять-таки «абстрактным», математическим пером: у этой кривой нет никакой толщины. Может случиться, что она разобьет шар на две области так, что в каждой из этих областей можно будет перейти от одной произвольной точки к любой другой, не пересекая нашу кривую.

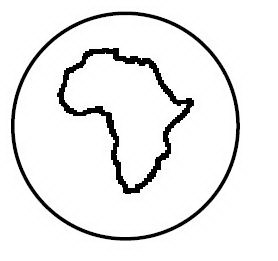
Вот пример такой кривой на шаре:

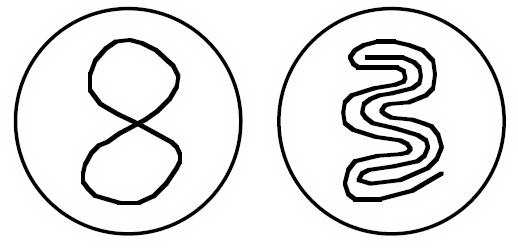
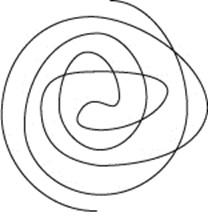
А вот примеры кривых на шаре, для которых рассматриваемое нами свойство не выполнено:

Итак, мы описали свойство кривой на шаре. (Точнее, как сказали бы математики, на сфере, потому что для математиков шар – это заполненная сфера.)

Вполне похоже, что обсуждаемое нами свойство является топологическим. Это значит, что если кривая разбивала сферу на две области, и мы сферу как-то деформировали, то деформированная кривая будет опять разбивать деформированную сферу на две области.

И действительно, если соответствующим (и естественным) образом определить все используемые математические понятия, то получится математическое определение топологического свойства, отвечающее нашим интуитивным представлениям.

Многие понятия топологии, обладая формальными математическими определениями, имеют весьма ясное интуитивное содержание. Более того, это содержание иногда относится к базовым понятиям, описывающим окружающий нас мир. Поэтому некоторые из этих понятий довольно часто появляются в курсах разных авторов – в учебниках и рабочих тетрадях для первого класса. Для нас задачи, включающие такой материал, являются частью начал образования, и заложенные в них идеи получают развитие на протяжении всего курса.

Кстати, приведем пример свойства, не являющегося топологическим: «Кривая ограничивает область, имеющую площадь 4 кв.см».

Лист определений «Считаем области»

Мы указали выше, что топология занимается фигурами и их свойствами, а не числами. Однако числа часто участвуют в определении тех или иных топологических свойств. Свойство, которое мы сейчас рассматриваем, тоже связано с числами. Это свойство – число областей в картинке. С самого начала при подсчете числа областей мы вводим цвет. На первый взгляд вам может показаться, что для подсчета числа областей вовсе не обязательно раскрашивать картинку. Но не спешите – так обстоит дело только в простейших случаях.

Как вы видите, при подсчете числа областей мы используем числовую линейку. При раскрашивании областей картинки (и клеток числовой линейки) мы используем все наши «рабочие» цвета, кроме черного. Черный цвет мы не используем из практических соображений – чтобы на клетках числовой линейки были виды все числа (черные), а на картинке – все черные внутренние линии. Цвета на числовой линейке (и в картинке) в какой-то момент начнут повторяться. Это не должно вызывать ошибок, если раскрашивание областей идет последовательно и аккуратно. При подсчете областей можно было бы обойтись даже одним цветом. Наличие нескольких цветов просто уменьшает возможные ошибки и позволяет допущенную ошибку исправить.

Итак, на листе определений описывается довольно несложное чередование действий: раскрашивание клетки числовой линейки – раскрашивание очередной области тем же цветом и т. д. Однако словесное описание этого несложного процесса ребенку порой понять нелегко. И дело не в том, что авторы не могут понятно описать простую вещь или специально хотят запутать непосвященных – проблема здесь в объективной ситуации: точные словесные описания весьма простых действий иногда оказываются сложными, и проще объяснить их на конкретном примере, как мы часто и делаем в нашем курсе.

Решение задач из учебника

Задача 17. Картинка в данной задаче несложная. Вы (а также, возможно, кто-то из детей) без всякой числовой линейки сосчитаете, сколько в ней областей. Но мы специально начинаем с простых задач, чтобы на их примере дети отработали алгоритм, описанный на листе определений. В противном случае дети, которые не усвоили общий алгоритм, со временем перестанут справляться с усложняющимся уровнем задач. В данной картинке 3 области, поэтому алгоритм закончится после третьего шага.

Кто-то из детей, возможно, спросит вас, что делать с глазами снеговика. Правильный ответ – не считать их областями, ведь на листе определений «Области» мы сразу договорились черный цвет не считать. Это одна из причин, почему мы ни в одном задании не предлагали (и в дальнейшем не будем) раскрашивать области картинки черным.

Задача 18. Как и в предыдущей задаче, областей в картинке немного и они хорошо выделяются. Особенность этой задачи состоит в том, что здесь картинка заключена в рамочку. Согласно нашим правилам все области, находящиеся внутри рамки, считаются областями картинки и должны учитываться при подсчете (об этом мы напоминаем и в условии задачи).

Задача 19. Эта задача на выделение русских букв и цифр из совокупности разнообразных знаков. Кто-то из ваших ребят возможно уже знает латинский (английский, французский и проч.) алфавит и может спросить, какой буквой следует считать букву «С» или «Н»  –  русской или нет. Ответ на этот вопрос довольно прост – русской нужно считать любую букву, которая есть в русском алфавите. Эта буква может быть и в алфавитах других языков, но в данной задаче это не имеет значения.

Задача 20. Если у кого-то из ребят с решением этой задачи возникнут проблемы, посоветуйте ему разделить бусины на группы по цветам и искать четыре одинаковые бусины среди бусин одного цвета.

Задача 21. В этой задаче ребята повторяют понятия «есть», «нет». В курсе 1 класса эти понятия чаще использовались для описания взаимоотношений элемента и мешка, но по отношению к элементу и цепочке они, конечно, употребляются в точности также (то есть, так же, как в языке).

Задача 22. Необязательная. Это первая задача, в которой число областей в картинке трудно определить визуально. На первый взгляд картинка в задаче выглядит довольно затейливой, за счет большого числа отрезков. Однако здесь всего 4 области, что хорошо видно после раскрашивания по ходу выполнения алгоритма подсчета областей.

Компьютерный урок «Считаем области»

Задачи на подсчет областей в компьютерном виде решать гораздо проще, чем на бумаге. Действительно, «заливка» полностью берет на себя всю нагрузку по выделению областей, за один щелчок всегда раскрашивая целиком ровно одно область. Поэтому если у вас есть возможность, удобно сразу после рассмотрения листа определений предложить детям решить одну-две компьютерные задачи на подсчет областей, а потом вернуться к работе с учебником. Поскольку в каждом компьютерном уроке имеется соответствующий лист определений, можно сразу посадить ребят за компьютеры – предложить им рассмотреть лист определений и решить задачи (все или выборочно), а после этого перейти к работе с учебником. В данном компьютерном уроке алгоритм подсчета областей на листе определений представлен в виде мультфильма, поэтому детям работать с компьютерным листом определений будет наверняка интересней.

Решение задач 25 – 32

Задача 25. Это первая компьютерная задача на подсчет областей картинки. Как видите, картинка для выделения областей довольно сложная, без поддержки «заливки» детям обойтись было бы затруднительно. Интересно, что, несмотря на большое число черных линий (границ областей), в этой картинке всего 4 области.

Задача 26. Если вы столкнетесь с ошибками такого типа, когда ребенок вообще не раскрашивает и не считает области фона, попросите ребенка вернуться к листу определений. Картинка с листа определений как раз в прямоугольной рамочке. Надо обратить внимание, что после подсчета областей на картинке не должно остаться ни одной нераскрашенной (белой) области. В этой картинке 7 областей – 5 областей фона и 2 области фигурки кота.

Задача 27. В этой задаче дети впервые строят мешок по описанию, данному с помощью набора утверждений, которые должны быть истинными. В процессе решения ребята повторяют понятие «мешок» из курса 1 класса и связанные с ним понятия «есть», «нет», «ровно». Так первое утверждение говорит о том, что в мешке ровно 2 медведя. Это значит, что в мешке есть 2 медведя, но нет трех. Второе же утверждение говорит, что в мешке есть 3 зайца. Это означает, что зайцев может быть как ровно 3, так и больше. Поскольку общее число фигурок в мешке не указано, подходящих мешков здесь может быть много. Например, в мешке, кроме двух медведей и нескольких (не меньше трех) зайцев, может быть несколько лис (птиц в мешке быть не должно).

Задача 28. Эта задача представляет определенный интерес с точки зрения различных случаев поиска объекта по описанию. Мы уже обращали ваше внимание, что в некоторых случаях условие выполняется для одного или нескольких объектов, иногда таких объектов вообще нет, а иногда условие выполняется для любого объекта. Так второе утверждение будет истинно для любой цепочки, в которой есть первая и вторая бусина. Среди данного набора цепочек оно для всех цепочек будет истинно, поэтому его добавление к первому утверждению ничего не меняет. Скорее всего, в вашем классе будут дети, которые начнут задавать по этому поводу недоуменные вопросы. Если таких ребят будет много, есть смысл организовать небольшое общее обсуждение данного случая. Самое простое – привести примеры аналогичных случаев из жизни. Например, поручить детям такое задание «Выбрать в классе всех ребят, которые изучают информатику».

Задача 29. В этой задаче ребята повторяют сравнение наложением. Конечно, дети не будут сравнивать наложением каждую фигурку с каждой, ведь некоторые кружки отличаются по размеру настолько сильно, что это хорошо видно на глаз. Скорей всего, дети будут сравнивать наложением только близкие по размеру фигурки. Именно среди таких фигурок учащиеся постепенно найдут две одинаковые кружки.

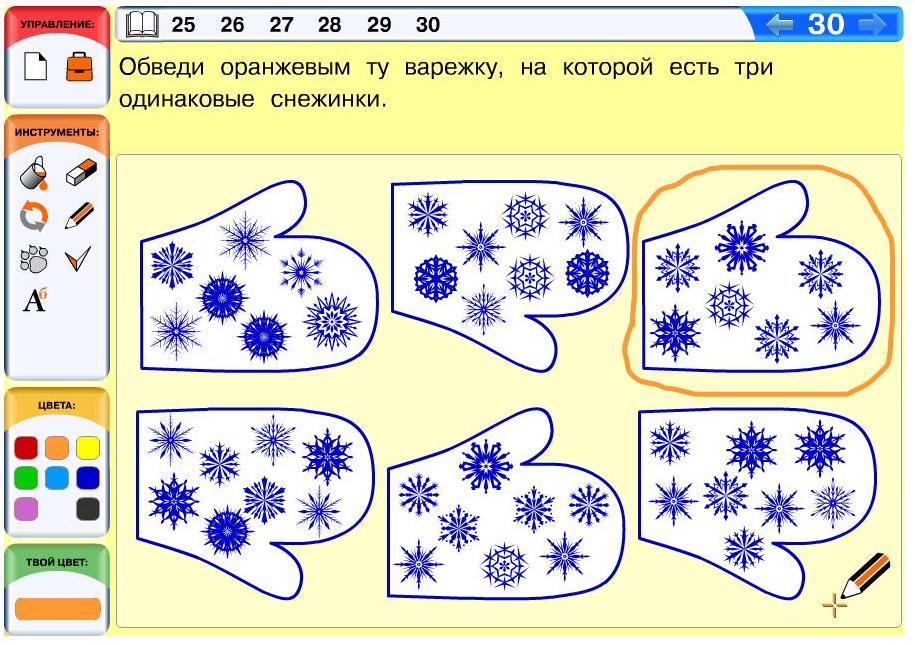
Задача 30. Необязательная. Здесь детям предстоит работать с реальными объектами – рукавицами, на которых нарисованы снежинки. Задача оказывается не слишком простой, ведь надо просмотреть каждую рукавицу и сравнить в ней снежинки между собой. При этом некоторые снежинки очень похожи и для такого сравнения требуется некоторое время. Так дети будут перебирать рукавицы, пока не отыщут искомую. С точки зрения понятий нашего курса данные объекты представляют собой мешки снежинок. Таким образом, в этой задаче дети повторяют понятие «мешок» и связанное с ним понятие «есть».

Проект «Снаружи и внутри» (для бескомпьютерного варианта изучения курса)

Практическая цель проекта — научиться выигрывать в игру «Верёвочка».

Методическая цель проекта — продолжение знакомства с топологическими понятиями («внутренняя область», «наружная область», «граница» и пр.), обучение построению информатической модели игровой ситуации.

В чём состоит игра?

Вы берёте верёвочку и раскладываете её на столе примерно так (вид сверху):

Потом вы предлагаете второму игроку (например, ребёнку) поставить палец в одну из петель верёвочки. При этом ваша задачу стянуть верёвочку двумя руками за два конца так, чтобы она не зацепилась за палец ребёнка.

Предварительная подготовка

Перед началом проекта от учителя потребуется некоторая подготовительная работа:

1. Запастись верёвкой. Самая лучшая — это верёвочка средней мягкости и средней толщины (3—6 мм). Длина верёвочки должна быть около 2 м (чем толще, тем длиннее). Лучше если верёвка будет из натурального материала.

2. Поиграть в эту игру с самим собой. Выкладывайте верёвку как угодно, следите только за тем, чтобы она сама себя не пересекала. Например, так класть верёвку не надо:

А так — очень даже можно:

3. Постарайтесь построить свою собственную теорию: как, глядя на верёвку на столе и палец, определить, зацепит ли верёвка палец при стягивании?

4. Как же использовать вашу теорию для организации описанной выше игры? Придумайте какой-нибудь сценарий и коротко запишите его. Когда вы всё это реально проделаете, можете читать дальше.

Теория игры в «Верёвочку»

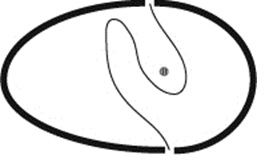
Когда человек взялся за концы верёвки, то его руки и тело вместе с верёвкой образуют замкнутую кривую. Для наших целей мы будем изображать человека просто толстым чёрным отрезком этой кривой:

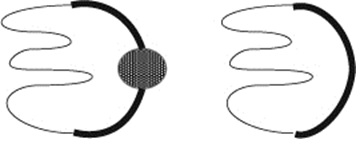
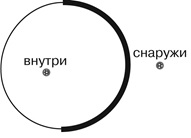
Как вы помните, мы кладём верёвку так, чтобы она никогда не пересекала себя, то есть наша замкнутая кривая должна быть без самопересечений. Замкнутая кривая без самопересечений на плоскости (в нашем случае на плоскости стола) разбивает эту плоскость на две части — внутри кривой и снаружи кривой. Изобразим палец ученика, поставленный на стол, просто жирной точкой:

Чтобы узнать, зацепится ли верёвка за палец, надо суметь определить, лежит ли точка внутри области или снаружи области. В простейшем случае все и так видно:

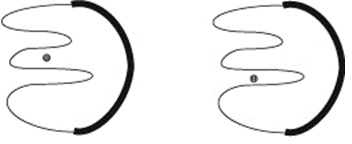
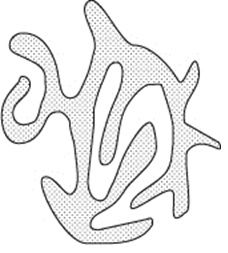
Вот более сложный случай:

Закрасим получившуюся область:

Пойдём из точки внутри области напрямик к какой-нибудь точке, лежащей снаружи:

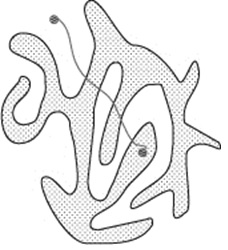
При этом мы будем пересекать нашу кривую несколько раз (переходя из закрашенной области в незакрашенную). Поэкспериментируйте и запишите на бумаге, сколько пересечений возникает.

При подсчёте вы, конечно, можете отказаться от верёвки и рисовать кривую на бумаге (не забывайте только, что кривая должна быть без самопересечения). Обратите внимание, что мы с вами уже перешли от телесной верёвки к более абстрактному графическому её представлению в виде кривой на бумаге.

Итак, какие числа у вас получились?

Получилось ли число 0, или 4, или 10?

Если да, посмотрите на свою картинку повнимательнее.

Итак, у вас получаются только нечётные числа: 1, 3, 5, 7, 9, 11, 13, 15…

Можем ли мы объяснить, почему?

Проследим, что происходит, когда мы идём по пути от внутренней точки к наружной. Пересекая нашу кривую первый раз, мы попадаем наружу (из серой области — в белую). Пересекая границу ещё раз, мы попадаем внутрь (в серую область) и т. д.:

Значит, если мы попадаем из серой области в белую, то число пересечений границ будет: 1 + 2 + 2 + … + 2, т. е. нечётным числом. Вот примеры картинок, которые могли у вас получиться:

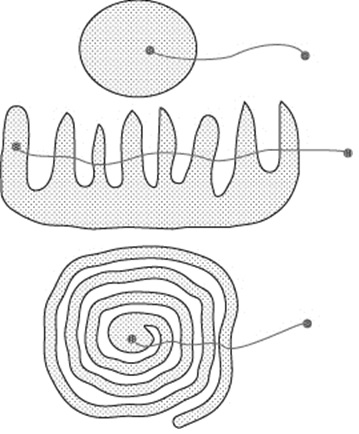
Пусть теперь мы начали из точки снаружи (из белой области) и пришли в белую же. Сколько раз мы пересекали нашу кривую? Вы, вероятно, уже поняли, что число пересечений может быть: 0, 2, 4, …

Вернёмся к исходной ситуации:

Идя от точки, расположенной внутри кривой, наружу, мы пересекаем нечётное число границ. Видя перед собой кривую, мы можем подсчитать число границ довольно легко. Это первое умение, которое нужно в нашей игре. Это, однако, ещё не всё. Ведь если ребёнок (пусть даже наугад) поставил палец внутрь кривой, нам не удастся сдёрнуть верёвку. Как тут быть?

Во всём обсуждении до настоящего места мы полностью (и сознательно) скрывали от вас одно обстоятельство. Оно состоит в том, что после того, как ребёнок поставил палец, вы можете взять верёвку за концы двумя различными способами:

При одном из этих способов точка окажется внутри, при другом — снаружи! Итак, поставив ребёнка у стола и выложив верёвку, как это описывалось раньше, мы оставляем за собой право выбора — подойти к столу справа или слева:

Теперь подытожим, все приведённые рассуждения. Чтобы правильно выбрать, с какой стороны стягивать верёвочку (если палец ученик уже поставил!), нужно сделать следующее:

1. Подойти с любой стороны (или просто это представить) и мысленно соединить концы верёвочки с этой стороны так, чтобы получилась замкнутая кривая без самопересечений.

2. Мысленно поставить точку с этой же стороны за проведённой границей кривой, то есть между проведённой линией и границей стола (листа, доски и пр.). Таким образом нужно поставить точку снаружи проведённой замкнутой кривой.

3. Сосчитать, сколько раз линия пересечёт кривую, если провести её от поставленной точки до пальца ученика (не забудьте посчитать и ту границу, которую вы мысленно провели!).

4. а) Если полученное число чётное, то палец ученика, как и выбранная точка, находится снаружи замкнутой кривой. Это означает, что верёвочку нужно стягивать как раз с той стороны, с которой мы подошли.
б) Если полученное число нечётное, значит, палец ученика стоит внутри проведённой кривой, и при стягивании с этой стороны верёвочка зацепится за палец. Это означает, что верёвочку нужно стягивать за концы, подойдя с другой стороны стола. Для проверки можно мысленно соединить концы верёвочки с другой стороны и снова провести аналогичные рассуждения.

Если, играя в «Верёвочку», палец ставите вы, то постарайтесь отрежиссировать ситуацию так, чтобы заранее знать, с какой стороны стола подойдет ребёнок. Значит, кроме математических знаний, нужно ещё некоторое искусство фокусника, «ловкость рук». Если дети постепенно начнут догадываться, что важно, откуда подходить, — это уже шаг к решению.

Ход проекта

Знакомство с игрой «Верёвочка»

Как и любой другой, данный проект должен начинаться с постановки практической цели. После этого ребята знакомятся с новой игрой. Лучше всего просто показать несколько партий. Для этого разложите верёвочку на столе. Напомним, верёвочка не должна пересекать сама себя, а изгибаться она может сколько угодно. Лучше вначале изгибать верёвочку так, чтобы игровая ситуация получалась не слишком простая. Теперь пригласите к доске кого-то из учащихся (лучше сильного ученика) и попросите поставить палец где-то между петель верёвочки. Объясните классу, что ваша задача стянуть веревочку за концы, не задев палец ребёнка. Конечно, у вас это получается. Теперь попросите ребёнка поставить палец в другое место и опять стяните верёвочку. Затем разложите верёвочку иначе и сыграйте ещё пару партий. После 3—4 партий у ребят начнёт складываться впечатление, что, как бы ни шла партия, игрок выигрывает всегда. Вот теперь поменяйтесь местами с ребёнком — разложите верёвочку, поставьте палец и попросите его стянуть верёвочку. Конечно, палец надо поставить так, чтобы у ребёнка не получилось стянуть верёвочку с наиболее удобной для него позиции. Если ребёнок догадается подойти с другого конца стола, значит, он уже уловил топологическую суть этой игры. Скорее всего, этого не произойдёт, и верёвочка зацепится за ваш палец. Так сыграйте с ребёнком ещё 2—3 партии. Учащиеся при этом заметят, что ребёнок гораздо чаще проигрывает. Так они догадаются, что учитель знает некий секрет, позволяющий в этой игре выигрывать. Можете в конце первого этапа урока озвучить эту мысль. Пообещайте ребятам, что в конце этого проекта ребята узнают этот секрет и сами смогут играть так, чтобы всегда выигрывать.

Парная игра в «Верёвочку»

Для начала предложите ребятам разбиться на пары и поиграть между собой. Проходя по классу, проверяйте, правильно ли ребята раскладывают верёвочку. В большинстве пар партии будут вначале проходить случайным образом — случайно выиграл или случайно проиграл. Однако сильные дети потихоньку начнут улавливать некоторые закономерности, особенно если верёвочку раскладывать, не слишком петляя. Чтобы оформить мысли сильных учащихся и заодно поддержать слабых, советуем вам по окончании этого этапа продолжить обсуждение игры «Верёвочка». Задача обсуждения — объяснить ребятам, какой выбор есть у того Игрока, который стягивает верёвочку. Как мы говорили, Игрок может взяться за концы верёвочки с одной стороны или подойти с противоположной стороны стола. В зависимости от этого игра приведёт к противоположному результату. Чтобы показать это, проведите ещё две партии у доски. Для этого возьмите две одинаковые верёвочки и разложите их на столе совершенно одинаково. Теперь пригласите к доске кого-то из учеников и попросите поставить в каждую верёвочку палец, так, чтобы пальцы стояли абсолютно одинаково. Можно вместо ученика использовать два одинаковых предмета, которые можно поставить в петли верёвочки, например, кусочек мела. Итак, получились две совершенно одинаковые исходные позиции. Теперь в первой позиции стяните концы верёвочки, подойдя с одной стороны, а во второй — с противоположной стороны. Ребята должны увидеть, что в одном случае вы выиграли, а в другом проиграли. Значит, стратегия Игрока в том, чтобы стягивать верёвочку, подходя с «правильной» стороны. Как же для любой партии увидеть эту правильную сторону? Отвечая на этот вопрос, стоит перейти к следующему этапу урока.

Решение задач 1—4 из тетради проектов

Для дальнейшего анализа игры «Верёвочка» необходимо, чтобы дети быстро и правильно умели определять, находится ли точка снаружи кривой или внутри неё. Именно для этого мы предлагаем им решить задачи 1—4 из тетради проектов. Эти задачи отличаются только сложностью кривой. Не обязательно решать все задачи, нужно решить столько задач, чтобы ребята начали понимать, как всё устроено и были готовы делать выводы.

После того как ребята поработали с задачами из тетради проектов, обсудите результаты одной из задач. Возьмите раскрашенную картинку и попросите ребят соединить две внутренние точки и посчитать, сколько раз линия пересекла границу. Теперь возьмите наружную и внутреннюю точки и попросите сделать их то же самое. Если необходимо, предложите ребятам несколько подобных заданий. В ходе выполнения у детей сформируется понимание, что при переходе от наружной точки к наружной (или от внутренней к внутренней) линия пересекает границу чётное число раз (в том числе и 0 раз), а при переходе от наружной точки к внутренней — нечётное. Значит, чтобы определить, является ли данная точка наружной или внутренней, раскрашивать картинку не обязательно — достаточно взять заведомо наружную точку (например, точку в самом углу рамки), соединить её с данной точкой и посчитать, сколько раз линия пересечёт границу кривой. На этот вывод нужно обратить внимание ребят.

Парная игра ребят в «Верёвочку»

Начать можно с одной партии у доски. Теперь уже можно сыграть с учеником, полностью раскрыв карты. Верёвочку следует уложить самым причудливым образом. После того как ребёнок поставит палец, подробно объясните свои действия, например, так: «Допустим, я хочу соединить концы вот с этой стороны. Тогда выберем снаружи от будущей кривой точку и будем двигаться от этой точки до пальца, считая, сколько раз мы пересечём верёвочку. Получилось 3 пересечения, значит, палец лежит внутри верёвочки и такой вариант нам не подходит. Значит, верёвочку надо стягивать за концы с другой стороны». После этого вы подходите с правильной стороны и стягиваете верёвочку, не задев пальца. Теперь поставьте палец в петли верёвочки и предложите ребёнку повторить ваши действия и рассуждения. После того как ему это удастся, можно переходить к парной работе.

Разбейте ребят на пары и предложите им сыграть несколько партий, по очереди выполняя действия Игрока. Теперь Игрок должен выигрывать всегда. Если в какой-то паре этого не происходит, с ней придётся поработать индивидуально, ещё раз показав и обсудив алгоритм.