Страницы сайта
Текущий курс
Участники
Общее
Тема 2
Тема 3
Тема 4
Тема 5
Тема 6
Тема 7
Тема 8
Тема 9
Тема 10
Тема 11
Тема 12
Тема 13
Тема 14
Тема 15
Тема 16
Тема 17
Тема 18
Тема 19
Тема 20
Тема 21
Тема 22
Тема 23
Тема 24
Тема 25
Тема 26
Тема 27
Тема 28
Тема 29
Урок 1. Комментарий для учителя к уроку «Истинные и ложные утверждения»
Урок 1. «Истинные и ложные утверждения»
Мы считаем, что эта тема важная не только для курса информатики и математики, но и для других школьных предметов и даже для дальнейшей жизни наших детей. Как видите, знакомство с истинными и ложными утверждениями начинается с простых и доступных примеров. Бывают ли в русском языке предложения, которые не являются утверждениями? Бывают, например: «Какая сегодня погода?» или «Приходи завтра». Это вопросительные предложения или предложения, в которых использовано повелительное наклонение. Мы, однако, не хотим сейчас фокусировать внимание ребенка на таких типах предложений.
Большинство заданий, которые выполняют дети в школе, изучая математику, языки и другие предметы, состоит в том, чтобы найти, построить объект, для которого истинно (т. е. выполняется, имеет место, верно) данное утверждение. Начиная работать с компьютером, учащиеся сразу же сталкиваются с понятием истинности утверждения при ответах на вопросы и при составлении простейших программ. Конечно, и в повседневной жизни ребенок, начав говорить, почти сразу сталкивается с понятием истинности. Его ругают, если он говорит неправду, когда он еще не вполне уяснил, что это такое.
Таким образом, понятие истинность встречается повсеместно. Конечно, можно пытаться не вводить это понятие явно, а считать само собой разумеющимся, используя множество синонимов – верно, правильно, подходит и т. д. Но нам кажется, что с самых разных точек зрения предпочтительнее явное введение понятия и фиксация термина, в качестве которого мы берем выражение истинное утверждение.
Явное введение понятия истинность делает более четким понятие решения математической задачи, которую теперь можно считать решенной вне зависимости от качества написания букв, скорости выполнения задания, поведения ученика и др. . Такое разделение нам кажется весьма желательным (в том числе и с социальной точки зрения – при воспитании молодых граждан, при усвоении ими их прав и обязанностей, законов, основ этики и т. д.).
Понятие истинность – краеугольное внутриматематическое понятие, используемое в построении математических теорий и систематическом введении языков, используемых в этих построениях. Свойство истинности утверждений для объектов – центральное свойство, изучаемое математической логикой.
Понятие ложное утверждение дети должны понимать как «не истинное». В обыденном языке в таких случаях говорится: неверное, неправильное, ошибочное и т. д. При построении объекта, для которого данное утверждение ложно, дети сталкиваются с необходимостью построения отрицания. Поскольку это довольно сложно, такие задачи будут попадаться детям не слишком часто (в основном в качестве необязательных).
Понятие истинности и ложности важно для нас не только с научной (содержательной) точки зрения, но и с точки зрения построения курса и наших правил игры. Постепенно формулировки задач становятся более сложными и объемными. Это затрудняет решение и проверку. Теперь из формулировки задачи детям приходится вычленять отдельные, простые условия, чтобы построить верное решение или сопоставить решение с условием задачи. Ясно, этот процесс сам по себе чреват ошибками. Поэтому описание объекта в виде совокупности отдельных утверждений, которые должны быть истинными (или ложными), – это возможность сделать условия задач более понятными, освободившись от всевозможных неточностей, которые привносит русский язык, когда мы пытаемся все эти условия сформулировать в 1 – 2 предложениях. Проверить истинность (ложность) утверждений также можно достаточно формально, последовательно одно за другим. Таким образом, истинность и ложность утверждений – это важная часть наших правил игры.
Обращаем ваше внимание, что наряду с обычными в математике значениями утверждений истинно и ложно мы используем еще одно – неизвестно. Это значение важно не только с информатической, но и с образовательно-психологической точки зрения. Нам важно привлечь внимание ребенка и ваше к тому, что на некоторые вопросы ответ неизвестен. Конечно, эта неизвестность может быть вызвана самыми разными причинами – недостаточностью информации, трудностью вопроса и пр. Все эти причины мы пока что помещаем в одну область – неизвестно. В дальнейшем, однако, дети сами заинтересуются разными видами неизвестности, и это может послужить материалом для интересной дискуссии. В контексте теоретической информатики значение неизвестно часто возникает, как это бывает и в жизни, когда ответ еще не получен, его поиск не закончен (а может быть, и не будет закончен никогда).
Отметим, что часто значение утверждения неизвестно бывает субъективным. Ситуация неизвестности часто связана с недостатком информации, причем кто-то этой информацией обладает, а кто-то нет. Безусловно, кто-то (например, авторы данной задачи) обладает информацией о том, как нарисована цепочка на листе определений и чему равен диаметр круглой бусины. Но детям эта информация, скорее всего, неизвестна. Кто-то из детей вообще может быть незнаком с понятием диаметр. Это не страшно, ведь в таком случае оценить истинность этого утверждения не представляется возможным и ответ «я не знаю» (соответствующий значению «неизвестно») является самым естественным.
По ходу изучения данного листа определений ребята повторяют понятие «цепочка» и понятия, связанные с порядком бусин в цепочке: первый, второй, третий, последний. Если вы хотите проверить, насколько ваши дети поняли материал листа определений, попросите их придумать несколько истинных и ложных утверждений о цепочке на листе определений. С примерами утверждений с неизвестным значением ребятам, возможно, придется помочь.
Решение задач из учебника
Задача 1. При возникновении затруднений в этой задаче следует попросить ребенка вернуться к листу определений и только самому слабому учащемуся можно предложить помощь в виде обсуждения утверждений. Цель этого обсуждения – сопоставить представления в голове ребенка с лексикой листа определений. Для начала следует попросить учащегося прочитать первое утверждение задачи, спросить, о какой бусине там говориться (о первой бусине цепочки) и попросить найти ее в цепочке. Затем следует спросить, правда ли (правильно ли, верно ли), что эта бусина треугольная? Да, верно, значит утверждение истинно. Надо пометить первое утверждение красной галочкой. Дальше можно обсудить второе и третье утверждение, а четвертое и пятое оставить для обдумывания ребенку. В этой задаче есть утверждение неизвестно, истинное или ложное – это третье утверждение.
Задача 2. По содержанию задача детям знакомая – им уже приходилось строить цепочку, удовлетворяющую условию (и даже двум-трем условиям). Но теперь такие задачи мы будем формулировать с помощью истинности (или ложности) утверждений, как в этой задаче, так их проще понять и решить. Надеемся, в вашем классе не найдутся дети, которые нарисуют цепочку из одной или двух бусин. В таком случае утверждение в задаче будет бессмысленно. Поэтому при возникновении таких проблем советуем просто обратить внимание ребенка, что утверждение никак не может быть истинным, поскольку третьей бусины в цепочке вообще нет.
Задача 3. В этой задаче необходимо построить цепочку так, чтобы утверждение было ложным. Такие задачи содержат в себе отрицание, поэтому, в сущности, тут можно идти двумя путями. Первый – явно словесно сформулировать истинное утверждения, имеющее то же значение, что ложность данного утверждения. В данном случае, истинным должно быть утверждение «Первая и третья бусина в этой цепочке разные». Однако словесно формулировать отрицание – дело непростое. Поэтому не стоит принуждать к этому детей, пусть каждый из детей подойдет к этому, когда будет готов. Есть и второй путь решения этой задачи – метод проб и ошибок. Например, можно построить для начала цепочку бусин как-нибудь. Но в ней обязательно должно быть хотя бы три бусины, иначе утверждение будет бессмысленно (а не ложно!). Затем следует определить истинность утверждения для нарисованной цепочки. Если утверждение будет ложным, то задача уже решена. Если оно будет истинным, то нужно исправить первую или третью бусину так, чтобы оно стало ложным.
Задача 4. Необязательная. Знакомая детям из курса 1 класса задача. Если такие задачи не удается решить хаотичным просмотром, то можно использовать разные стратегии, в том числе, полный перебор или разбиение фигурок на группы. Можно разбить все фигурки по цвету одного из квадратиков, например, верхнего левого. Групп получилось четыре, причем в двух группах по одной фигурке. Значит, осталось сравнить две фигурки с желтым квадратиком и три фигурки с голубым квадратиком.
Задачи 5-6. Прежде всего, нужно внимательно прочитать данное в задаче утверждение и понять его смысл. Как обычно, мы советуем вам не обсуждать задачу сразу со всеми детьми, поэтому многие дети будут вначале строить цепочку как-нибудь, то есть решать методом проб и ошибок. В ходе этих проб у детей будет формироваться представление о том, что должно получиться. Такой способ не хуже любого другого, но чтобы не было грязи в тетради, посоветуйте детям сначала соединить все фигурки в цепочку простым карандашом, затем проверить истинность (или ложность) утверждения и только потом провести соединительную линию фломастером или ручкой.
Задача 7. Необязательная. Задача посвящена конструированию объекта по образцу. После решения полезно выполнить проверку, предварительно обсудив с ребятами, как это сделать. Чтобы убедиться в правильности выполнения задания, нужно сравнить соответствующие элементы левой и правой фигур, двигаясь по определенной системе, например, сверху вниз и слева направо.
Задача 8. Эта задача аналогична задаче 1 и листу определений. Поэтому если у кого-то из детей на уроке на нее не хватит времени, то ее можно предложить на дом. Среди данных утверждений ровно два истинных, три ложных, утверждений с неизвестным значением в данной задаче нет.
Задача 9. Необязательная. Мы надеемся, что эта задача покажется детям довольно привлекательной и даст им возможность в конце урока немного расслабиться и отдохнуть. Однако она преследует и важную методическую цель. На примере этой задачи дети смогут увидеть, что истинные и ложные утверждения не являются какой-то специфической частью нашего курса, их можно строить относительно любого объекта, который имеет место в школьном предмете или окружающем мире. Так в этой задаче все утверждения относятся к приведенной картинке. Картинка в свою очередь относится к сказке Пушкина «О царе Салтане», но для решения это не имеет значения. Мы умышленно не используем в курсе тех практических или прикладных задач, для решения которых необходимы какие-то специфические знания, ведь дети могут такими знаниями по каким-то причинам не обладать. Например, далеко не все современные дети оказываются знакомы даже с такими общеизвестными сказками как «Колобок» или «Курочка Ряба». Поэтому в задаче нет утверждений относящихся к сюжету сказки, все утверждения относятся только в данной картинке. Среди данных утверждений три истинных и два ложных.
Компьютерный урок «Повторение»
Данный компьютерный урок полностью посвящен повторению курса 1 класса. Здесь дети повторяют наиболее простой материал – основные атомарные объекты курса: фигурки, бусины, буквы и цифры, а также понятия «одинаковые/разные» для этих объектов. Кроме того дети на данном уроке повторяют все основные компьютерные инструменты, введенные в курсе 1 класса: «заливку», «карандаш», «галочку», «лапку». С сильными и подготовленными классами этот урок вполне можно пропустить. Со слабыми детьми он будет, безусловно, полезен. Данный урок позволит ребятам быстро войти в материал, начав с простых задач.
Решение задач 1 – 8
Задача 1. Здесь ребята вспоминают понятие «одинаковые фигурки». Если ребенок испытывает затруднения, посоветуйте ему, либо полный перебор фигурок, либо разбиение фигурок на группы по наличию/отсутствию некоторого цвета. В этой задаче дети вспоминают компьютерный инструмент «пометь галочкой». Возможно, найдутся ребята, которым в индивидуальном порядке придется напомнить последовательность действий – щелкнуть мышкой кнопку «галочка», выбрать в палитре подходящий цвет, щелкнуть мышкой в том месте экрана, где хотим поставить галочку.
Задача 2. Здесь ребята вспоминают инструмент «заливка», соответствующий действию «раскрась». Напомним, чтобы залить некоторую область, нужно щелкнуть по инструменту «заливка» в ящике инструментов, выбрать соответствующий цвет и щелкнуть по нужной области. В подобных задачах раскрашенные в условии квадратики перекрасить нельзя. Удобнее всего двигаться по строкам (или столбцам) двух фигур одновременно, сравнивая квадратики на соответствующих местах. В данной задаче в каждой паре квадратиков один квадратик окажется раскрашенным, а другой – нет. Значит, нераскрашенный квадратик надо раскрасить в такой же цвет. Если ребенок начал раскрашивать квадратики хаотично и в какой-то момент совсем запутался, проще будет проще начать решение сначала.
Задача 3. Аналогичные задачи встречались ребятам в курсе 1 класса. Решать ее наобум (методом проб и ошибок) оказывается довольно долго и затруднительно – необходим хотя бы минимальный анализ исходных фигур. Для начала есть смысл просмотреть исходные фигуры и понять, есть ли среди них хотя бы две одинаковые. Оказывается, есть, значит можно попробовать поискать нераскрашенную фигурку такой же формы и размера. Такая фигурка отыскивается, значит именно ее нужно раскрасить в тот же цвет, что и две одинаковые фигурки.
Задача 4. Объектов здесь довольно много – может понадобиться перебор. Конечно, в первом задании перебор нужно вести только по русским буквам, а во втором – только по цифрам. Умение выделять из совокупности русские буквы для решения этой задачи является ключевым, поскольку здесь в наборе имеются пары одинаковых латинских букв. Если ученик выделил пару латинских букв, необходимо вернуться вместе с ним к листу определений «Русские буквы и цифры» из курса 1 класса и попросить его найти помеченные им в задании буквы в русском алфавите.
Задача 5. В этой задаче дети впервые в курсе 2 класса используют инструмент «карандаш». При этом некоторым детям оказывается трудно вести непрерывную линию, поскольку нужно одновременно следить и за проведением линии на экране и за работой руки. Если у кого-то из ребят провести непрерывную линию не получится с первого раза, вполне допустимо составить ее из нескольких кусочков. Стереть линию можно как обычно «ластиком». Если на экране много линий-кусочков, лучше использовать кнопку «начать сначала».
Задача 6. В этой задаче ребята вспоминают понятие «одинаковые бусины». Если кто-то из учащихся испытывает трудности при решении этой задачи, посоветуйте ему разбить бусины на группы по цвету (или по форме). Также полезно использовать здесь пометки. Одну или две группы бусин можно выделить и рассмотреть вместе с учащимся. Например, в наборе ровно 4 синие бусины, среди которых лишь две одинаковые, значит, все синие бусины можно вычеркнуть или пометить галочкой и перейти к бусинам другого цвета.
Задача 7. В этой задаче ребята впервые в курсе 2 класса используют инструмент «лапка». Если ребенок забыл особенности его работы, можно попросить его открыть урок «Положи в окно» в курсе 1 класса, где работа «лапки» на листе определений и в первых задачах описана подробно.
Задача 8. Необязательная. Последние задачи в каждом уроке у нас чаще всего необязательные. Задачи, подобные этой, в курсе 1 класса мы советовали предлагать детям для развлечения или по желанию тем, кто любит рисовать и раскрашивать. В начале года есть смысл предложить задачу всем, она быстро позволит ребятам вспомнить все особенности работы заливки. В частности, раскрашивая мелкие области, ребята вспомнят о необходимости прицеливаться крестиком заливки, чтобы попасть в нужную область.
Компьютерный урок «Истинные и ложные утверждения»
В ходе выполнения данного компьютерного урока ребята закрепляют материал текущего листа определений. Напомним, что при компьютерном варианте изучения курса средний учащийся не всегда будет успевать решить все обязательные задачи как из учебника, так и из соответствующего компьютерного урока. Поэтому учитель должен предложить всему классу такой набор задач, который максимально органично дополняет задачи из учебника, но не дублирует их. Остальные задачи можно предложить на дом или просто пропустить.
Решение задач 9 – 16
Задача 9. В этой задаче требуется выделить из набора все истинные утверждения и неизвестно истинные или ложные утверждения. Проще всего это сделать, по очереди перебирая утверждения и выясняя, какое оно (истинное, ложное или неизвестно истинное или ложное).
Задача 10. В этой задаче ребята продолжают повторять понятие «цепочка», но наиболее важным для решения этой задачи является усвоение понятий «все», «каждый». В частности, для решения здесь необходим полный перебор всех цепочек, причем в каждой цепочке необходим полный перебор всех круглых бусин. Только при таком способе решения можно найти ответ гарантированно.
Задача 11. В данном случае свинью можно поставить в любое окно кроме первого, в этом дети могут убедиться методом проб и ошибок. После этого перед свиньей нужно поставить оленя. Поскольку про остальные фигурки цепочки в описании не сказано ничего, их можно расставлять в окна как угодно. Таким образом, подходящих цепочек здесь довольно много.
Задача 12. Данная задача сложнее предыдущей, ведь здесь утверждение должно быть не истинным, а ложным. Кто-то из детей в состоянии мысленно построить отрицание, в сущности, сделать это не слишком сложно. То, что третья и последняя фигурки одинаковые должно быть не верно (ведь утверждение ложно), значит, третья и последняя фигурки в цепочке должны быть не одинаковыми, то есть – разными. Дети, которые не в состоянии провести подобные рассуждения, легко решат задачу методом проб и ошибок.
Задача 13. Здесь в описании уже не одно, а два утверждения, которые должны быть истинными. Как видите, все утверждения относятся не к порядку бусин в цепочке, а лишь к составу бусин в цепочке. Поэтому если у кого-то из ребят решение не идет, посоветуйте ему, сначала собрать комплект бусин, из которых потом будет строиться цепочка. Потом нужно обсудить этот набор, проверив, что бусин действительно три, что все они красные, что среди них нет одинаковых. При нарушении одного из условий нужно просить ребенка менять набор. После того как нужные бусины подобраны, можно ставить их в цепочку в любом порядке.
Задача 14. В этой задаче ребята повторяют сравнение фигурок наложением. Фигурки здесь настолько похожи, что большинство ребят будут проводить полный перебор. Если соединять фигурки в пары по ходу решения, то постепенно приходится перебирать все меньшее число фигурок.
Задача 15. Задача на выделение из набора русских букв и цифр. При возникновении ошибок в различении символов необходимо побуждать ребенка обратиться к листу определений «Русские буквы и цифры» из курса 1 класса. Заметим, что в наборе всего 7 русских букв, то есть требуется выделить не все русские буквы, а указанное число. Если кто-то из детей ошибается в этом, напомните учащемуся одно из принятых в курсе правил игры – не делать больше того, что написано в задании.
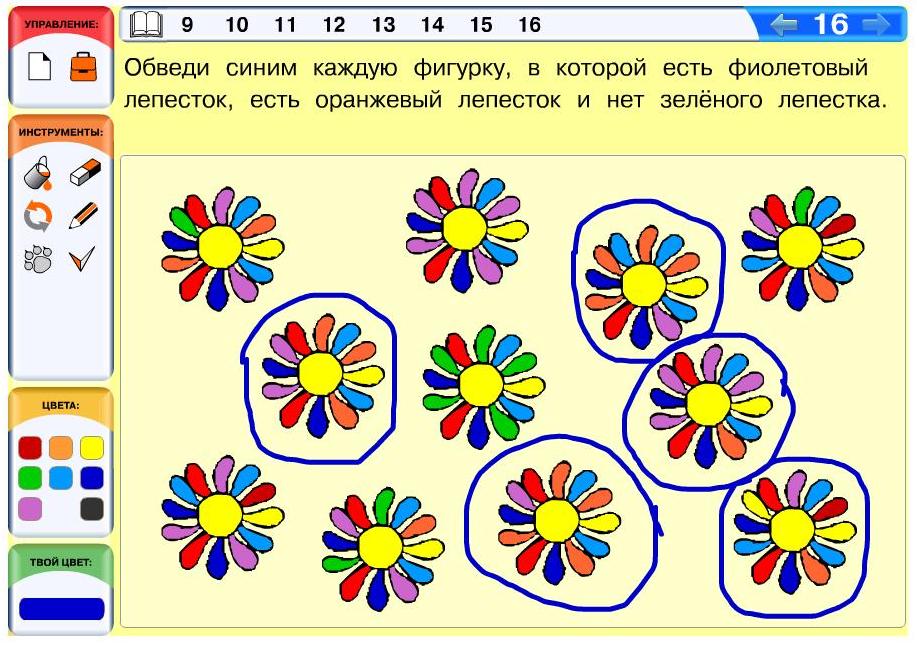
Задача 16. Необязательная. На первый взгляд эта задача скорей развлекательная, но с точки зрения системы понятий нашего курса она является довольно сложной. Как видите, в ней использовано одновременно несколько важных понятий курса: «каждый», «есть», «нет». Если вы видите, что ребенок в ней совсем запутался, проведите с ним некоторую часть перебора вместе, например, просмотрите верхнюю строку цветков и обведите все цветы, соответствующие условию. Затем попросите учащегося аналогично поработать со второй строкой самостоятельно и проверьте результат. Чтобы ничего не пропустить, можно как обычно помечать все просмотренные цветки, например, галочкой.