Информатика. 1 класс Демо+методичка

Урок 30. «Таблица для мешка»

Новые ключевые слова и выражения: таблица для мешка, рабочая таблица для мешка.

Важнейшей целью курса информатики является формирование у ребят информационной культуры, в частности информационной компетентности. Одна из главных составляющих информационной компетентности – умение работать с информацией, представленной в разных видах: рисунок, текст, схема, таблица и т.д. Таким образом, умение работать с таблицей (понимать нарисованную таблицу, а также создавать ее самостоятельно) – важная часть информационной культуры. На данном уроке мы знакомим учащихся с тем, как можно использовать таблицу для классификации. В этом году дети будут проводить классификацию только по одному признаку, поэтому и таблицы для мешка будут пока одномерными. В шапке таких таблиц будут указываться все значения выбранного признака. Чаще шапка будет располагаться горизонтально (в строке), но это совершенно необязательно; шапку можно разместить и вертикально, если это удобнее. В примере, рассмотренном на листе определений, признаком является тип (внешний вид) бусины. Здесь бусины не рассматриваются отдельно по форме и цвету, а просто в шапке изображаются все разные бусины, которые есть или могут быть в мешке. В таблице даются, в частности, бусины, которых в мешке вообще нет. В таком случае в соответствующей клетке будет стоять ноль. Заметим, что в таблице должны быть обязательно представлены все значения выбранного признака, которые есть в мешке. Что же касается значений, которых в мешке нет, они могут быть указаны полностью или частично, а могут и вовсе отсутствовать. В любом случае у ребят это вопросов не вызовет, поскольку они чаще всего будут работать с таблицами, шапка которых уже заполнена, то есть все нужные значения признаков уже указаны. Ясно, что для одного мешка зачастую можно заполнить несколько одномерных таблиц – по разным признакам. Так, для мешка бусин кроме описанной на листе определений таблицы можно заполнить еще две одномерные таблицы классификации – по форме и по цвету.

На листе определений заполняется сначала рабочая таблица, а затем уже таблица для мешка. Это позволяет объяснить ребятам  алгоритм учета элементов мешка. Действительно, если в мешке небольшое число элементов, которые легко различаются, проблема заполнения таблицы для мешка не встает. Но если элементов в мешке много и они похожи (например, в мешке лежит много мелких греческих букв), то очень легко сбиться и допустить ошибку. Поэтому лучше сразу познакомить ребят с алгоритмом, который позволит безошибочно заполнить таблицу для мешка вне зависимости от количества и специфики объектов в мешке. Этот алгоритм состоит в следующем. Выбираем любой элемент в мешке и проделываем с ним следующие действия: 1) помечаем его галочкой; 2) помечаем в рабочей таблице крестиком клетку, соответствующую значению выбранного признака у данного элемента. Выбираем другой элемент в мешке и проделываем с ним пункты 1 и 2. И так далее, пока все элементы мешка не окажутся помеченными. Заполнение рабочей таблицы позволяет не сбиться, даже если ребенок в какой-то момент отвлекся, ведь алгоритм можно продолжить с любого места. После того как рабочая таблица будет заполнена, несложно посчитать число крестиков в каждом столбце и заполнить таблицу для мешка.

Решение задач из учебника

Задача 169. В этой первой задаче очень важно добиться от всех детей, чтобы они следовали описанному на листе определений алгоритму. Поэтому, если ребенок заполнил только таблицу для мешка и больше у него в решении нет никаких пометок, нужно вернуть его к листу определений и попросить заполнить сначала рабочую таблицу (даже если таблица заполнена верно). Очень важно учить детей следовать алгоритму, это, как и работа с таблицей, важная часть информационной культуры.

Ответ:

Задача 170. В отличие от таблицы для мешка бусин на листе определений, таблица в этой задаче не определяет мешок однозначно. В частности, в таблице содержится информация только о форме бусин в мешке, но ничего не говорится о цвете этих бусин. Поэтому цвет может быть любым, например в мешке все 6 бусин могут быть красными.

Задача 171. Предложите ребятам решить эту задачу самостоятельно от начала и до конца, не давая никаких подсказок. На все вопросы ребят вы, скорее всего, уже ответили в ходе решения задачи 169. Кроме того, пример заполнения аналогичной таблицы для мешка рассматривается на листе определений.

Ответ:

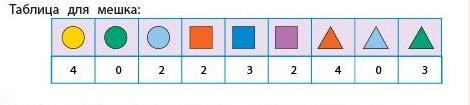
Задача 172. Необязательная. В случае затруднений в этой задаче посоветуйте учащемуся разбить мешки на две группы по наличию или отсутствию в мешке некоторой фигурки, например слона с хоботом, поднятым вверх.

Задача 173. Данная задача внесет разнообразие в мир абстрактных бусин и букв и в то же время даст представление о возможности классификации объектов, далеких от математики. Здесь ребятам предстоит классифицировать достаточно большое число фигурок. Запутавшемуся ученику можно предложить помечать в мешке посчитанных мышек, главное, чтобы для двух таблиц пометки были разными. Необходимо закончить решение проверкой: парной, с обязательным установлением истины и совместным поиском всех ошибок, или самопроверкой, состоящей из двух этапов. Первый этап – сравнение общего числа мышек в мешке и в таблицах. Различие в какой-либо паре чисел говорит о наличии ошибки, совпадение же этих чисел еще не гарантирует верного результата. Чтобы убедиться в правильности ответа наверняка, необходимо снова пересчитать мышек с каждым означенным в таблице признаком.

Ответ:

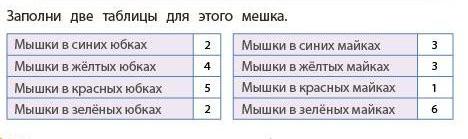
Задача 174. Необязательная. Эта задача может оказаться еще сложнее предыдущей, особенно если решать их подряд. В задаче 173 ребята ориентируются только на два признака, и они по ошибке могут осуществить неправильный перенос этого правила на задачу 174. На самом деле кроме цвета майки и юбки здесь необходимо еще принимать во внимание цвет бантика и позу самой мышки. Тем не менее полезно использовать какой-либо признак, чтобы разбить мышек на группы и не осуществлять полный перебор, сравнивая мышек между собой. Например, можно отдельно сравнивать мышек в синих майках, затем в красных и т. д.

Конечно, удобнее всего было бы искать одинаковых мышек, если бы их можно было вырезать и разложить на кучки (так дети искали одинаковых мышек в проекте «Разделяй и властвуй»). Возможно, именно так вы и предложите выполнить задачу 174 дома по желанию. В таком случае всем желающим нужно выдать откопированный мешок с мышками, попросить их дома вырезать всех мышек и, разложив на группы по определенным признакам, найти двух одинаковых (а затем обвести их в мешке).

Вот решение данной задачи:

Задача 175. Лучше никаких предварительных пояснений учащимся не давать, а в случае затруднений возвращать ребят к текущему листу определений. Наверняка у вас найдутся ребята, которые упорно будут заполнять таблицу для мешка без использования рабочей таблицы и какого бы то ни было алгоритма. С такими детьми придется поработать индивидуально и объяснить им полезность формальных алгоритмов.

Ответ:

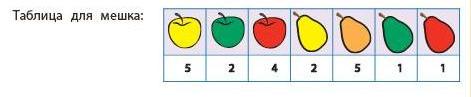
Задача 176. Необязательная. Интересно, что в этой задаче первая фраза условия играет двоякую роль. Основное ее предназначение  – общеразвивающее. У многих детей есть замечательное свойство – любознательность, им интересно, что это за закорючки, что они могут означать и т. д. Мы будем развивать и поощрять это качество. Но догадливый ребенок может использовать первую фразу и как подсказку. Действительно, исходя из лингвистических соображений, можно провести аналогии между звуковым и буквенным рядом слова (по аналогии с родным языком) и сделать вывод, что одинаковыми будут буквы, которые одинаковы по звучанию. Конечно, это не всегда так (и в русском, и в других языках), но в данном случае это работает, и одинаковые буквы находятся совсем быстро.

Задача 177. В этой задаче проверяется усвоение важных логических понятий «каждый» и «есть» (нет). Ребята к настоящему моменту уже должны понимать, что любое задание со словом «каждый» подразумевает полный перебор объектов. Значение словосочетания «есть три прямоугольника» дети должны отличать от «ровно три прямоугольника». Второе означает, что в мешке есть 3 прямоугольника, но нет четырех, а первое – что в мешке есть хотя бы три прямоугольника. Поэтому в первом задании нам подойдут и мешки, в которых больше трех прямоугольников, например второй или последний. Всего подходящих мешков в первом задании оказывается четыре. Во втором задании подходящих мешков оказывается ровно два.

Задача 178. Необязательная. Аналогичные задачи ребятам уже встречались (см. комментарий к задаче 148). Здесь лучше всего просматривать элементы по порядку, начиная с первого во всех трех цепочках сразу. Так, в одной из цепочек первая буква – А, значит, такую же букву надо написать в пустых окнах на первом месте в остальных двух цепочках. Дальше аналогично работаем со вторыми элементами цепочек, затем – с третьими и так, пока все окна во всех цепочках не будут заполнены.

Задача 179. Необязательная. Многие дети в подобных задачах предпочитают придумывать слова русского языка, и подходящие слова здесь найти несложно, например: МАМА, ПАПА, ТЫ, МЫ, ВЫ, КАШКА, КОРОТКО, КАРТОШКА, КАРАМЕЛЬКА, ОКОРОК и проч.  Однако заметим, что здесь совсем необязательно придумывать «осмысленные» слова, ведь по условию достаточно составить цепочку букв, соответствующую описанию. Так, в качестве решения подойдут цепочки букв: ЛОТНЛО, АРШНГАР и проч.

Компьютерные уроки «Таблица для мешка»

1 часть

Задача 187. Здесь дети работают по алгоритму, показанному на листе определений. Чтобы поставить крестик, дети используют инструмент «карандаш».

Задача 188. В этой задаче ребятам предстоит проделать операцию, обратную заполнению таблицы для мешка, а именно достроить мешок по таблице. В данном случае таблица представляет классификацию бусин по цвету. Чтобы при решении задачи не запутаться, лучше следовать некоторой системе работы. Например, рассматривать клетки таблицы по очереди и помечать уже использованные клетки.

Задача 189. В этой задаче крайне сложно найти мешок случайно, хаотичным просматриванием. Поэтому, так или иначе, придется выполнять перебор. Это можно делать по-разному. Первый способ – брать по очереди мешки и проверять для них всю таблицу. Второй способ – брать по очереди строки таблицы и проверять их сразу для всех мешков. Если некоторая строка не соответствует одному из мешков, то этот мешок выбрасывается из дальнейшего рассмотрения. Видим, что в каждом мешке есть по две красные фигурки, значит, первая строка таблицы справедлива для всех мешков. В первом мешке лишь одна оранжевая фигурка, значит, первый мешок нам не подходит. Теперь рассмотрим оставшиеся строки таблицы для трех оставшихся мешков. Во всех этих мешках есть 3 желтые и одна зеленая фигурки. Однако в последнем мешке нет голубой фигурки, значит, он тоже не подходит. Таким образом продолжаем анализировать мешки до тех пор, пока у нас не останется только один мешок.

Вот решение данной задачи:

Задача 190. Как и в большинстве задач со словом «все», здесь требуется полный перебор слов и проверка для каждого из них обоих условий, данных в задаче. Как всегда в задачах подобного рода, встает вопрос об очередности проверки условий. В данном случае решающим фактором будет то, что первое условие проверить гораздо проще, чем второе. Поэтому сначала проверяем его. Оказывается, что оно выполняется для всех слов, кроме слова МОЛОКО, которое вычеркиваем. Далее проверяем второе условие. Оно выполняется для слов ПРИМЕТА и МЕЛОЧЬ.

Задача 191. Наверняка ваши дети уже хорошо знают числовой ряд до 20. Числовая линейка здесь приведена не в качестве справки, а скорей для графической опоры, чтобы детям легче было учитывать числа, которые они уже просмотрели в мешке. При этом удобно помечать просмотренные числа и в мешке, и на числовой линейке. Когда в мешке числа закончатся, на числовой линейке останется одна неотмеченная клетка, в которой и будет стоять искомое число. Можно помечать одинаковые числа в мешке и на числовой линейке галочкой или обводить, а можно соединять их в пары.

Задача 192. В этой задаче существует много решений. В частности, две одинаковые фигурки в цепочке можно сделать из второй и третьей фигурок, из последней и первой фигурок либо из последней и предпоследней.

Задача 193. В этой задаче довольно длинное условие, требующее внимательного прочтения (прослушивания) и анализа. После того как дети поймут условие, они увидят, что изначально в задаче все наоборот – крайние мешки разные, а средний и правый – одинаковые. Большинство ребят догадаются, что сначала лучше заняться крайними мешками. Кому-то при этом будет удобно соединить уже имеющиеся пары одинаковых бусин. После этого для каждой свободной бусины из левого мешка нужно положить такую же бусину в правый мешок и наоборот. При этом желательно помечать уже учтенные бусины, чтобы не сбиться. После того как мы выполним первое условие, второе условие будет выполняться автоматически, и средний мешок можно вообще не трогать. Конечно, это лишь одна из возможных стратегий, дети могут использовать и другие, в том числе не самые рациональные.

Задача 194. Необязательная. Если у кого-то из ребят возникли трудности с этой задачей, посоветуйте ему метод полного перебора.

2 часть

Задача 195. В этой задаче дети строят мешок бусин по таблице. В отличие от таблицы, которую дети видели на листе определений «Таблица для мешка» (и в компьютерной задаче 187), здесь бусины в шапке таблицы указаны не графически, а с помощью описаний.

Задача 196. В отличие от компьютерной задачи 187, где дети сначала заполняли рабочую таблицу, а потом таблицу для мешка, здесь рабочей таблицы нет. На самом деле без нее вполне можно обойтись, т.к. фигурки в мешке различаются существенно, да и по количеству их не слишком много. Однако ребята уже должны понимать, что необходима некоторая система работы, чтобы не запутаться. Ну и конечно, чтобы ничего не упустить, желательно использовать пометки. Заполняем первую клетку таблицы – считаем число помидоров в мешке. Для этого лучше всего сначала пометить все помидоры, например синей галочкой. Затем считаем количество помеченных фигурок и записываем это число в таблицу. Теперь считаем количество баклажанов, предварительно пометив все баклажаны галочками. Для наглядности лучше использовать галочки другого цвета, например зеленые. Так действуем до тех пор, пока клетки в таблице не закончатся. После этого нужно убедиться, что все фигурки в мешке помечены галочками. Если остались непомеченные фигурки, нужно скорректировать числа в соответствующих клетках таблицы.

Задача 197. Это довольно сложная задача, поскольку в ней ребятам придется работать одновременно с двумя таблицами для одного мешка. Проблема в том, что с этими таблицами нельзя работать независимо, например сначала собрать мешок, удовлетворяющий первой таблице, а потом доработать его так, чтобы он удовлетворял второй таблице. Поэтому придется учитывать информацию сразу двух таблиц. Это можно делать по-разному, и подходящих мешков здесь будет очень много. Вот один из вариантов. Видим из первой таблицы, что в мешке должно быть 4 груши, а из второй – что в мешке должно быть 4 красные фигурки. Положим в мешок 4 красные груши. Из первой таблицы видим, что в мешке должно быть 2 банана, а из второй – что в мешке должно быть 2 зеленые фигурки. Положим в мешок 2 зеленых банана. Теперь из второй таблицы видно, что остальные 6 фигурок в мешке должны быть желтыми. Это 5 яблок и 1 слива. По окончании решения попросите ребят сделать проверку – заполнить две таблицы для получившегося мешка.

Вот одно из решений данной задачи:

Задача 198. Для правильного выполнения задания важно понять, что в мешке не должно быть одинаковых фигурок. Согласно таблице в мешке должно быть 4 ежа, значит, все 4 ежа должны быть разными – оранжевый смотрящий вправо, оранжевый смотрящий влево, голубой смотрящий вправо и голубой смотрящий влево. Аналогично, необходимо проследить, чтобы в мешке не было одинаковых зайцев и одинаковых белок (белки должны быть только голубыми).

Вот одно из решений данной задачи:

Задача 199. Здесь одинаковые фигурки можно найти и без наложения, поэтому использовать «лапку» будут, в основном, те ребята, которым это нравится. Остальным можно посоветовать выполнить наложение для проверки, однако обязательно нужно предложить это сделать ребятам, допустившим ошибки.

Задача 200. Ребятам, которые ошиблись в этой задаче, нужно посоветовать выполнить полный перебор, используя при этом пометки. Если выбранное число идет позже 6, значит, его можно сразу обвести, если нет – можно его пометить галочкой. Наибольшее число вопросов здесь будет связано с числом 6. Конечно, число 6 помечать не нужно, ведь оно идет не позже самого себя, но причина ошибок в том, что учащиеся считают отрицанием понятия «позже» понятие «раньше». «Не позже значит раньше», – часто говорят ребята. Однако «раньше» и «не позже» – это разные понятия, постепенно в ходе решения задач ребятам предстоит это понять.

Задача 201. Задача комбинаторного типа, в которой помимо прочего проводится пропедевтика понятия «все разные». Не стоит в таких задачах помогать ребенку чрезмерно – достаточно просто указать на ошибку. Если кто-то из ребят не знает, с чего начать, посоветуйте ему воспользоваться методом проб и ошибок. Бусины первого мешка можно раскрасить в желтый и голубой цвета как угодно. Бусины второго мешка можно тоже раскрашивать не слишком задумываясь – достаточно, чтобы второй мешок отличался от первого. Третий мешок сначала можно тоже раскрасить произвольно, а затем сравнить его с первым и вторым. Если третий мешок оказался таким же, как первый (или второй), достаточно изменить в нем цвет хотя бы одной бусины. Если после этого он стал таким же, как другой мешок, достаточно изменить цвет другой бусины. Аналогичным образом будем действовать, пока условие задачи не будет выполнено. Однако, возможно, в классе найдутся дети, которые будут решать эту задачу логически. На самом деле рассуждения учащихся могут быть достаточно несложными. Например: в первый мешок положим 3 желтых бусины, во второй – две, в третий – одну, в четвертый – ни одной. В каждом мешке все остальные бусины раскрасим голубым. Уже сама эта схема делает очевидным тот факт, что среди мешков не будет двух одинаковых.

Вот решение данной задачи (с точностью до порядка мешков):

Задача 202. Необязательная. Эта задача больше понравится детям, которые любят раскрашивать. Вряд ли эта задача покажется детям сложной – им уже не раз приходилось раскрашивать фигурки, чтобы сделать их одинаковыми. Разными фигурки сделать еще проще – нужно хотя бы одну область в двух фигурках раскрасить в разные цвета.