Информатика. 1 класс Демо+методичка

Урок 16. «Все, каждый»

Новые ключевые слова и выражения: все, каждый, все остальные.

Понятие все является вторым из наиболее важных понятий математической информатики, с которыми ученики знакомятся в нашем курсе. (Первым было понятие одинаковости.)

Надеемся, что ученикам понятия все, каждый покажутся простыми. Они и на самом деле простые (например, «каждый его знает»). Однако не всегда это было так. Например, постижение силлогизмов Аристотеля составляло существенную часть средневекового высшего образования. Возможно, вы встречали и примеры силлогизмов вроде:

                                 Все люди смертны.

                                 Сократ – человек.

                                 _______________________________________

                                 Следовательно, Сократ смертен.

Надеемся, что ученики без труда будут в будущем строить рассуждения такого рода. Но предостерегаем вас от игнорирования того, что понимание детьми таких «очевидных» слов, как, например, каждый, поначалу может немного или даже существенно отличаться от вашего.

Слова все, каждый всегда относятся к некоторой совокупности объектов. Иногда эта совокупность устроена сложно: все атомы во Вселенной или все действительные числа. Мы довольно долго будем иметь дело с простыми совокупностями, умещающимися на одной странице, где объекты сравнительно легко перебрать по одному.

Именно такой перебор (по одному) и нужно осуществлять каждый раз, когда мы выполняем какое-то действие или проверяем какое-то свойство для всех объектов. Не надо формулировать это в виде правила. Лучше, если дети будут относиться к словам все, каждый просто как к словам русского языка с очевидным смыслом. Однако желательно проверить, все ли дети (опять все!) правильно понимают этот смысл и действительно в какой-то мере систематически просматривают все объекты. Это очень важно для формирования информатического, конструктивного взгляда на понятия и процессы.

Просмотр объектов

В нашем курсе мы стараемся сделать наглядными, видимыми объекты информатики (а также математики и лингвистики), так же как и отношения между ними и действия над ними. Такая визуализация объектов информатики, сочетание образного и символического описаний очень продуктивны в обучении. Они же являются одним из основных направлений развития информационных технологий в целом и их применения в образовании – в частности. Все чаще и чаще, рассказывая что-то друг другу, люди одновременно показывают это на экране, куда проецируется компьютерное изображение, где появляются все необходимые иллюстрации.

Речь пойдет об одном важном умении: просматривать и сортировать графические или символьные объекты, расположенные в некотором поле (скажем, на странице или в поле одной задачи). В жизни такое умение необходимо везде, начиная от чтения меню, расписания движения поездов и самолетов, географических карт и заканчивая поиском подходящих туфель на полке магазина. Возможно, в предыдущих задачах некоторые ребята уже пытались осуществить просмотр объектов, однако без него можно было и обойтись. В последующих задачах полный и систематический просмотр объектов становится необходимым условием решения задачи.

Процедура просмотра, которую обычно использует ребенок, а часто и взрослый, хаотическая. Это – беспорядочное перескакивание взгляда с одного предмета на другой. Иногда эта стратегия не так уж плоха. Однако она не годится в тех случаях, когда требуется выполнить действительно полный просмотр, или, как иногда говорят в информатике и математике, полный перебор. Поэтому необходимо вычеркивать или обводить уже просмотренный объект или хотя бы ставить на нем (или вблизи него) точку. Но если ребенок не использует графических пометок, перечисленных выше, полезно предложить ему некоторую стратегию просмотра. (Например, просматривать объекты в ряду слева направо, переходя к следующему ряду сверху вниз.) Использование этой стратегии можно облегчить с помощью линейки, которую надо перемещать сверху вниз, каждый раз просматривая появившиеся целиком над линейкой объекты. Эта стратегия требует большой аккуратности и хорошо работает, если объекты расположены по строкам.

Через несколько лет на уроках информатики детям придется составлять программы для компьютера, включающие полный просмотр, сортировку объектов и другие важные операции. Мы хотим, чтобы дети хорошо понимали, что это значит, и умели это делать вручную. Иначе как они смогут сознательно обучить этому компьютер?

Решение задач из учебника

Задача 78. Дети уже встречались с понятием «инструкция» в задаче 67. Но если в задаче 67 порядок выполнения действий не влиял на результат, то здесь нарушение последовательности выполнения пунктов инструкции ведет к ошибкам и даже отказам. Например, если учащийся выполнит сначала второй пункт инструкции, а затем – третий, то первый пункт он после этого выполнить просто не сможет – в наборе не останется бусин для раскрашивания. Таким образом, в этой задаче вам, возможно, придется обсудить с кем-то из детей, что такое инструкция и как ее необходимо выполнять.

Задача 79. Проследите за тем, чтобы ребенок не забыл выполнить проверку (это последняя строчка задания), даже если он абсолютно уверен в правильности своего решения (это опять соблюдение правил игры). Проверка заключается в том, чтобы осуществить полный перебор всех оставшихся на листе вырезания фигурок и убедиться, что это не улитки.

Задача 80. Эта задача напоминает задачу 78. Однако здесь результаты выполнения отдельных заданий не связаны между собой, поэтому их можно выполнять в любом порядке и даже одновременно. Например, взять любую бусину, определить ее форму, прочитать в условии, каким цветом надо раскрашивать бусины такой формы, раскрасить ее этим цветом и перейти к другой бусине. Так будем делать до тех пор, пока все бусины не будут раскрашены. Это один из алгоритмов выполнения данного задания, но не самый быстрый. Дети быстрее выполнят пункты задания по порядку, тогда им не придется постоянно возвращаться к условию задачи.

Задача 81.  Обратите внимание на эту задачу, она является важной с разных точек зрения. С одной стороны, данная задача поддерживает курс арифметики – здесь детям придется вспомнить названия некоторых цифр. С другой стороны, здесь впервые дети используют инструментальное действие «соедини» не для выделения пары объектов, а для установления соответствия между двумя группами объектов.  Понятие «соответствие» лежит в основе многих разделов математики, в частности теории функций. В данном случае ситуация совсем простая – нужно установить соответствие между набором цифр и набором слов (названий этих цифр). Соответствие при этом является взаимно-однозначным – каждой цифре можно сопоставить ровно одно слово и наоборот. Несмотря на глубину теоретической подоплеки данной задачи, думаем, у детей она никаких вопросов не вызовет. Поэтому, хоть задача и является для ребят совершенно новой, советуем не давать им никаких общих пояснений. Как и любая другая задача со словами «все, каждый», эта задача должна заканчиваться проверкой, включающей полный перебор. Необходимо еще раз просмотреть каждую цифру и проверить, что от нее идет линия к некоторому слову. 

Задача 82. Условно говоря, мы конструируем фигурку по образцу, точнее – мы конструируем три фигурки, при этом для каждой из них образцом являются две другие. Действительно, чтобы раскрасить правильно первую фигурку, нужно посмотреть, в какие цвета раскрашены в других фигурках ее пустые клеточки (фиолетовый, голубой, желтый). То же самое надо проделать с двумя другими фигурками. Однако стратегия решения может быть иной: можно каждую клеточку анализировать только один раз – сразу в трех фигурках. Последний способ более эффективен.

Задача 83. В задаче используются буквы латинского алфавита, правда в витиевато-декоративном начертании. Здесь ребята оценивают одинаковость латинских букв как фигурок.

Задача 84. Необязательная. Как видите, здесь нужно создать набор объектов (бусин) по описанию, которое содержит отрицание («чтобы не было двух одинаковых бусин»). Конечно, чтобы выполнить это задание, совсем необязательно анализировать и понимать утверждение на уровне формальной логики. Эту задачу можно решать методом проб и ошибок, то есть для начала просто наобум. Нарисуем 8 нераскрашенных круглых бусин. Раскрасим две бусины разными цветами, ведь если мы раскрасим их одинаковыми цветами, то у нас сразу появятся две одинаковые бусины. Теперь раскрасим третью бусину так, чтобы она не была ни такой, как первая, ни такой, как вторая. Для этого ее надо раскрасить цветом, отличным от цвета первой и второй бусин. Так можно раскрашивать бусины и дальше, поверяя на каждом шаге, не появилось ли в наборе двух одинаковых раскрашенных бусин.

Задача 85. Необязательная. В этой задаче детям необходимо помнить, что зеркально симметричные фигурки являются разными.

Вот решение  данной задачи:

Задача 86. Необязательная. Если у кого-то из ребят с решением возникнут проблемы, посоветуйте ему разделить бусины на группы по цветам и искать три одинаковые бусины среди бусин одного цвета.

Компьютерный урок «Все, каждый»

Задача 79. Первая задача, как обычно, несложная. Хотя объектов на экране много, арбузы очень сильно отличаются от остальных фигурок своей черно-зеленой раскраской (то есть буквально бросаются в глаза), поэтому выделить их в совокупности совсем нетрудно. Если все же ребенок ошибся и обвел не все арбузы, то, скорее всего, это связано с тем, что он плохо усвоил новое понятие. В этом случае учащегося следует вернуть к листу определений «Все, каждый» (в учебнике или в компьютерном уроке).

Задача 80. В отличие от предыдущей, задачи здесь яблоки не бросаются в глаза, и детям придется их действительно искать. Если при этом кто-то сделает ошибку, поместив в окно не все яблоки, попросите его рассказать, как он искал яблоки. Возможно, ребенок применил стратегию полного перебора, но просто в какой-то момент отвлекся и пропустил яблоко. Если же он искал яблоки беспорядочно, то в этом случае ненавязчивая беседа с учителем должна навести его на следующую мысль: чтобы не пропустить ни одного яблока, надо просмотреть все фигурки. Вполне возможно, что до остального он додумается сам: как сделать так, чтобы при просмотре не пропустить ни одной фигурки? Может, помечать просмотренные? А может, просто двигаться методично от фигурки к фигурке и от ряда к ряду?

Задача 81. В этой задаче проблема полного перебора впервые становится действительно актуальной. Хаотичным просматриванием ребенок, скорее всего, найдет только часть искомых фигурок. Но это еще не все. Как мы уже говорили выше, только полный перебор даст учащимся уверенность в том, что они нашли все буквы, отвечающие условию задачи. Заметим, что поскольку фигурки в задаче располагаются хаотично, то при переборе желательно использовать пометки. При этом вовсе необязательно просматривать буквы в том или ином порядке. Ребенок может выхватывать их взглядом в произвольном порядке, главное, чтобы он помечал каждую просмотренную букву: либо обводил (если она отвечает условию задачи), либо зачеркивал (если буква не отвечает условию). В этом случае задача будет решена, как только все буквы окажутся либо зачеркнутыми, либо обведенными. Разумеется, после того как решение будет найдено, все лишние линии надо удалить с помощью «ластика».

Задача 82. Для начала каждый ребенок должен разобраться, что от него требуется в этой задаче. В условии речь идет о треугольных бусинах, поэтому возьмем любую треугольную бусину, например желтую. Бусину нужно соединить с яблоком того же цвета, значит, соединяем ее с желтым яблоком. В условии не сказано, каким цветом при этом пользоваться, поэтому выбираем любой, например желтый. В условии сказано, что эту процедуру надо проделать для каждой треугольной бусины, следовательно, мы должны перебрать все бусины. Обнаружив вторую зеленую треугольную бусину, ребенок может запнуться. Надо ли ее соединять? Ответ: надо, потому что мы должны соединить КАЖДУЮ треугольную бусину с яблоком. В итоге получится, что с зеленым яблоком будут соединены две бусины, а с красным – ни одной.

Задача 83. Технически эта задача не из самых легких. Здесь надо провести семь соединительных линий – от каждой бусины к названию ее цвета. Сложность состоит в том, что в задаче мало свободного места, к тому же названия цветов располагаются довольно тесно. Поэтому при решении задачи учащимся придется быть предельно аккуратными и внимательными, чтобы было понятно, какие линии что и с чем соединяют. Чтобы решение было более наглядным, посоветуйте им проводить соединительные линии разными цветами. Наиболее интересным было бы такое решение, при котором соединительная линия имеет тот же цвет, что и бусина, которую она соединяет со словом.

Задача 84. Если ребенок допустил в задаче ошибку, попросите его проверить свое решение. Для этого, прежде всего, следует понять, что мы должны проверять. Исходя из условия, если задача решена правильно, то должны быть верными следующие четыре утверждения: а) в правом окне находятся только треугольные бусины; б) в левом окне находятся только круглые бусины; в) вне окна нет круглых бусин; г) вне окна нет треугольных бусин. Разумеется, приведенные выше рассуждения являются формальными, и обсуждать их с ребенком не следует. Однако многие дети могут заметить, что, решая эту задачу, мы фактически осуществляем сортировку бусин по форме: в результате все круглые бусины оказываются в одном окне, все треугольные – в другом, все квадратные – «за окном». Это важное наблюдение, и крайне желательно, чтобы учащиеся сделали его самостоятельно. Если ребенок допустил ошибку и не понимает, как проверить свое решение, попытайтесь ему помочь наводящими вопросами. Например: «Посмотри, все ли треугольные бусины ты положил в окно?» «Не положил ли ты в окно чего-нибудь лишнего?» И так далее.

Задача 85. Здесь, как и в задаче 84, можно попросить учащихся выполнить проверку своего решения. Было бы полезно обсудить с каждым учеником индивидуально, какие шаги он должен предпринять, чтобы убедиться в правильности своего решения (или же выявить ошибку). В действительности проверка решения этой задачи состоит из двух шагов. Первое: проверить, не осталось ли круглых бусин, которые ни с чем не соединены. Второе: проверить все пары соединенных бусин, в каждой из них бусины должны быть одинакового цвета, но разной формы – одна круглая, а другая треугольная.

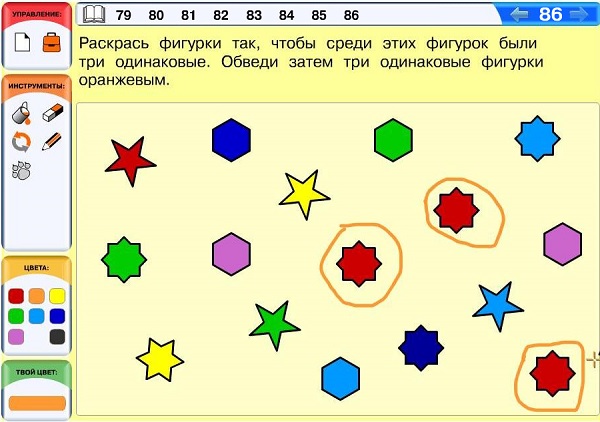
Задача 86. Необязательная. Эта задача аналогична компьютерной задаче 37, только немного сложнее – здесь больше фигурок и больше разных форм. Однако ситуация здесь в точности такая же, как в задаче 37. Среди раскрашенных фигурок одинаковых нет, но есть две одинаковые нераскрашенные фигурки – восьмиконечные звезды. Ученик может раскрасить их голубым, синим, красным или зеленым – каждое из этих решений будет правильным.

Вот одно из решений данной задачи: